带花树算法(Blossom Algorithm)
开花算法(Blossom Algorithm,也被称做带花树)可以解决一般图最大匹配问题(maximum cardinality matchings)。此算法由 Jack Edmonds 在 1961 年提出。 经过一些修改后也可以解决一般图最大权匹配问题。 此算法是第一个给出证明说最大匹配有多项式复杂度。
一般图匹配和二分图匹配(bipartite matching)不同的是,图可能存在奇环。
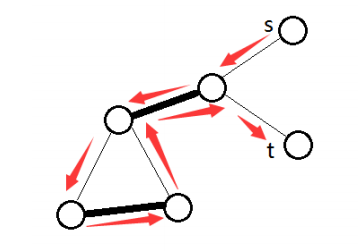
以此图为例,若直接取反(匹配边和未匹配边对调),会使得取反后的 不合法,某些点会出现在两条匹配上,而问题就出在奇环。
下面考虑一般图的增广算法。 从二分图的角度出发,每次枚举一个未匹配点,设出发点为根,标记为 「o」,接下来交错标记 「o」 和 「i」,不难发现 「i」 到 「o」 这段边是匹配边。
假设当前点是 ,相邻点为 ,可以分为以下两种情况:
- 未拜访过,当 是未匹配点,则找到增广路径,否则从 的配偶找增广路。
- 已拜访过,遇到标记「o」代表需要 缩花,否则代表遇到偶环,跳过。
遇到偶环的情况,将他视为二分图解决,故可忽略。缩花 后,再新图中继续找增广路。
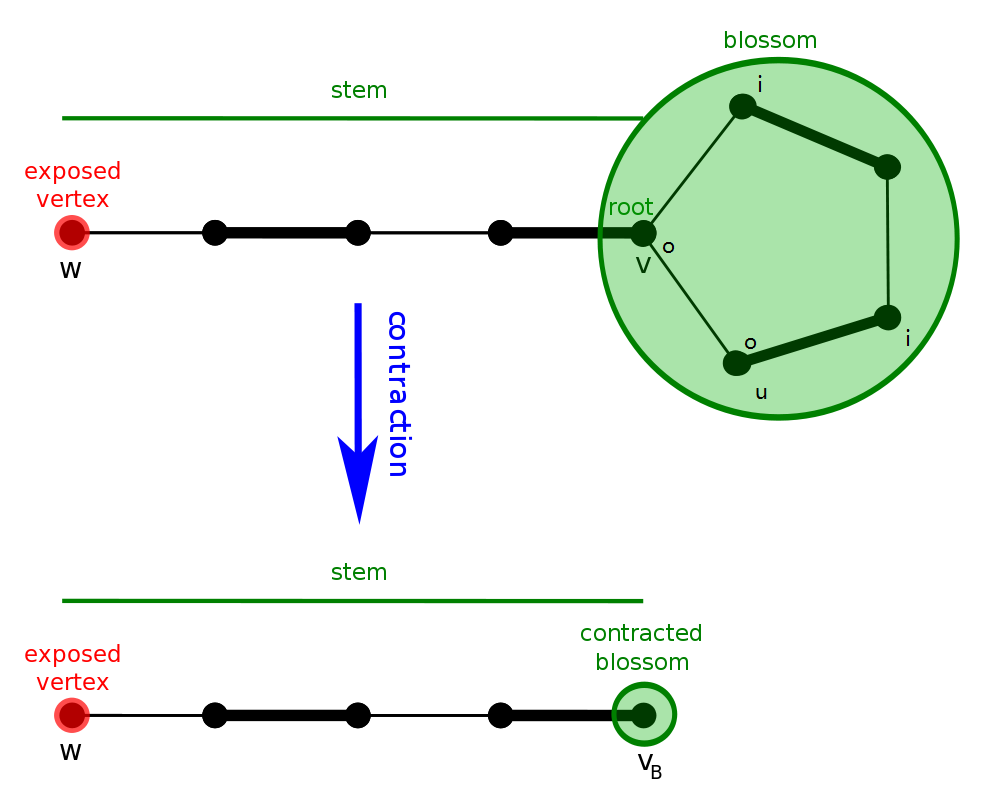
设原图为 ,缩花 后的图为 ,我们只需要证明:
- 若 存在增广路, 也存在。
- 若 存在增广路, 也存在。
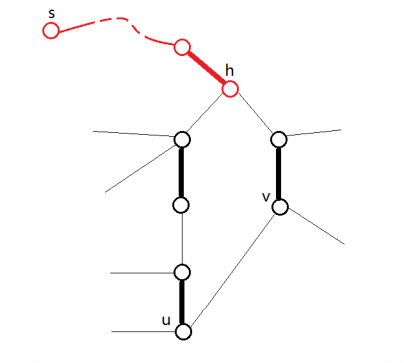
设非树边(形成环的那条边)为 ,定义花根 。 奇环是交替的,有且仅有 的两条邻边类型相同,都是非匹配边。 那么进入 的树边肯定是匹配边,环上除了 以外其他点往环外的边都是非匹配边。
观察可知,从环外的边出去有两种情况,顺时针或逆时针。
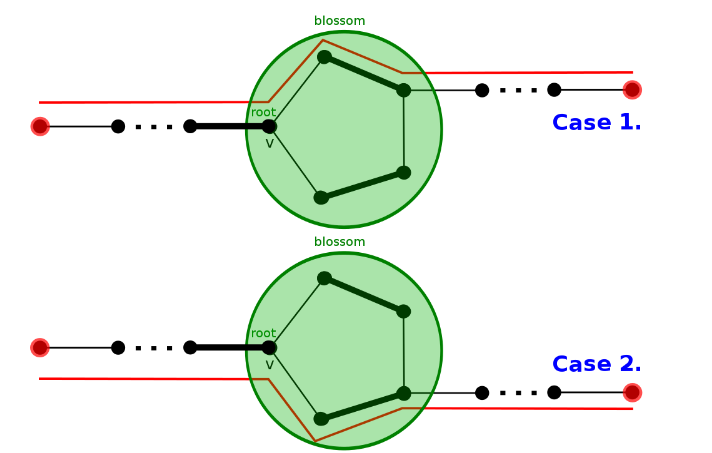
于是 缩花 与 不缩花 都不影响正确性。
实作上找到 花 以后我们不需要真的 缩花,可以用数组纪录每个点在以哪个点为根的那朵花中。
复杂度分析 Complexity Analysis
每次找增广路,遍历所有边,遇到 花 会维护 花 上的点,。
枚举所有未匹配点做增广路,总共 。
参考代码
参考代码
// graph template <typename T> class graph { public: struct edge { int from; int to; T cost; }; vector<edge> edges; vector<vector<int>> g; int n; graph(int _n) : n(_n) { g.resize(n); } virtual int add(int from, int to, T cost) = 0; }; // undirectedgraph template <typename T> class undirectedgraph : public graph<T> { public: using graph<T>::edges; using graph<T>::g; using graph<T>::n; undirectedgraph(int _n) : graph<T>(_n) {} int add(int from, int to, T cost = 1) { assert(0 <= from && from < n && 0 <= to && to < n); int id = (int)edges.size(); g[from].push_back(id); g[to].push_back(id); edges.push_back({from, to, cost}); return id; } }; // blossom / find_max_unweighted_matching template <typename T> vector<int> find_max_unweighted_matching(const undirectedgraph<T> &g) { std::mt19937 rng(std::random_device{}()); vector<int> match(g.n, -1); // 匹配 vector<int> aux(g.n, -1); // 时间戳记 vector<int> label(g.n); // 「o」或「i」 vector<int> orig(g.n); // 花根 vector<int> parent(g.n, -1); // 父节点 queue<int> q; int aux_time = -1; auto lca = [&](int v, int u) { aux_time++; while (true) { if (v != -1) { if (aux[v] == aux_time) { // 找到拜访过的点 也就是LCA return v; } aux[v] = aux_time; if (match[v] == -1) { v = -1; } else { v = orig[parent[match[v]]]; // 以匹配点的父节点继续寻找 } } swap(v, u); } }; // lca auto blossom = [&](int v, int u, int a) { while (orig[v] != a) { parent[v] = u; u = match[v]; if (label[u] == 1) { // 初始点设为「o」找增广路 label[u] = 0; q.push(u); } orig[v] = orig[u] = a; // 缩花 v = parent[u]; } }; // blossom auto augment = [&](int v) { while (v != -1) { int pv = parent[v]; int next_v = match[pv]; match[v] = pv; match[pv] = v; v = next_v; } }; // augment auto bfs = [&](int root) { fill(label.begin(), label.end(), -1); iota(orig.begin(), orig.end(), 0); while (!q.empty()) { q.pop(); } q.push(root); // 初始点设为「o」,这里以「0」代替「o」,「1」代替「i」 label[root] = 0; while (!q.empty()) { int v = q.front(); q.pop(); for (int id : g.g[v]) { auto &e = g.edges[id]; int u = e.from ^ e.to ^ v; if (label[u] == -1) { // 找到未拜访点 label[u] = 1; // 标记「i」 parent[u] = v; if (match[u] == -1) { // 找到未匹配点 augment(u); // 寻找增广路径 return true; } // 找到已匹配点 将与她匹配的点丢入queue 延伸交错树 label[match[u]] = 0; q.push(match[u]); continue; } else if (label[u] == 0 && orig[v] != orig[u]) { // 找到已拜访点 且标记同为「o」代表找到「花」 int a = lca(orig[v], orig[u]); // 找LCA 然后缩花 blossom(u, v, a); blossom(v, u, a); } } } return false; }; // bfs auto greedy = [&]() { vector<int> order(g.n); // 随机打乱 order iota(order.begin(), order.end(), 0); shuffle(order.begin(), order.end(), rng); // 将可以匹配的点匹配 for (int i : order) { if (match[i] == -1) { for (auto id : g.g[i]) { auto &e = g.edges[id]; int to = e.from ^ e.to ^ i; if (match[to] == -1) { match[i] = to; match[to] = i; break; } } } } }; // greedy // 一开始先随机匹配 greedy(); // 对未匹配点找增广路 for (int i = 0; i < g.n; i++) { if (match[i] == -1) { bfs(i); } } return match; }
#include <algorithm> #include <cassert> #include <iostream> #include <numeric> #include <queue> #include <random> #include <vector> using namespace std; // graph template <typename T> class graph { public: struct edge { int from; int to; T cost; }; vector<edge> edges; vector<vector<int>> g; int n; graph(int _n) : n(_n) { g.resize(n); } virtual int add(int from, int to, T cost) = 0; }; // undirectedgraph template <typename T> class undirectedgraph : public graph<T> { public: using graph<T>::edges; using graph<T>::g; using graph<T>::n; undirectedgraph(int _n) : graph<T>(_n) {} int add(int from, int to, T cost = 1) { assert(0 <= from && from < n && 0 <= to && to < n); int id = (int)edges.size(); g[from].push_back(id); g[to].push_back(id); edges.push_back({from, to, cost}); return id; } }; // blossom / find_max_unweighted_matching template <typename T> vector<int> find_max_unweighted_matching(const undirectedgraph<T> &g) { std::mt19937 rng(114514); // 这里随机种子是无关紧要的 // 也可以用 chrono::steady_clock::now().time_since_epoch().count() // 获取当前时间 vector<int> match(g.n, -1); // 匹配 vector<int> aux(g.n, -1); // 时间戳记 vector<int> label(g.n); // "o" or "i" vector<int> orig(g.n); // 花根 vector<int> parent(g.n, -1); // 父节点 queue<int> q; int aux_time = -1; auto lca = [&](int v, int u) { aux_time++; while (true) { if (v != -1) { if (aux[v] == aux_time) { // 找到拜访过的点 也就是LCA return v; } aux[v] = aux_time; if (match[v] == -1) { v = -1; } else { v = orig[parent[match[v]]]; // 以匹配点的父节点继续寻找 } } swap(v, u); } }; // lca auto blossom = [&](int v, int u, int a) { while (orig[v] != a) { parent[v] = u; u = match[v]; if (label[u] == 1) { // 初始点设为"o" 找增广路 label[u] = 0; q.push(u); } orig[v] = orig[u] = a; // 缩花 v = parent[u]; } }; // blossom auto augment = [&](int v) { while (v != -1) { int pv = parent[v]; int next_v = match[pv]; match[v] = pv; match[pv] = v; v = next_v; } }; // augment auto bfs = [&](int root) { fill(label.begin(), label.end(), -1); iota(orig.begin(), orig.end(), 0); while (!q.empty()) { q.pop(); } q.push(root); // 初始点设为 "o", 这里以"0"代替"o", "1"代替"i" label[root] = 0; while (!q.empty()) { int v = q.front(); q.pop(); for (int id : g.g[v]) { auto &e = g.edges[id]; int u = e.from ^ e.to ^ v; if (label[u] == -1) { // 找到未拜访点 label[u] = 1; // 标记 "i" parent[u] = v; if (match[u] == -1) { // 找到未匹配点 augment(u); // 寻找增广路径 return true; } // 找到已匹配点 将与她匹配的点丢入queue 延伸交错树 label[match[u]] = 0; q.push(match[u]); continue; } else if (label[u] == 0 && orig[v] != orig[u]) { // 找到已拜访点 且标记同为"o" 代表找到"花" int a = lca(orig[v], orig[u]); // 找LCA 然后缩花 blossom(u, v, a); blossom(v, u, a); } } } return false; }; // bfs auto greedy = [&]() { vector<int> order(g.n); // 随机打乱 order iota(order.begin(), order.end(), 0); shuffle(order.begin(), order.end(), rng); // 将可以匹配的点匹配 for (int i : order) { if (match[i] == -1) { for (auto id : g.g[i]) { auto &e = g.edges[id]; int to = e.from ^ e.to ^ i; if (match[to] == -1) { match[i] = to; match[to] = i; break; } } } } }; // greedy // 一开始先随机匹配 greedy(); // 对未匹配点找增广路 for (int i = 0; i < g.n; i++) { if (match[i] == -1) { bfs(i); } } return match; } int main() { ios::sync_with_stdio(false); int n, m; cin >> n >> m; undirectedgraph<int> g(n); while (m--) { int u, v; cin >> u >> v; g.add(u - 1, v - 1); // 0-based } auto match = find_max_unweighted_matching(g); cout << count_if(match.begin(), match.end(), [](int x) { return x != -1; }) / 2 << endl; for (int i = 0; i < n; i++) cout << match[i] + 1 << " \n"[i == n - 1]; return 0; }
基于高斯消元的一般图匹配算法
提示
这一部分将介绍一种基于高斯消元的一般图匹配算法。与传统的带花树算法相比,它的优势在于更易于理解与编写,同时便于解决「最大匹配中的必须点」等问题;缺点在于常数比较大,因为高斯消元的 基本是跑满的,而带花树一般跑不满。
前置知识:Tutte 矩阵
定义:对于一张 个点的无向图 ,其 Tutte 矩阵 为一个 的矩阵,其中:
其中 是一个变量,因此 中共有 个变量。
在无歧义的情况下,以下将 简写为 。
定理(Tutte 定理): 存在完美匹配当且仅当 。
证明
这里引入「偶环覆盖」的概念:一个无向图 的偶环覆盖指用若干偶环(包括二元环)不重不漏地覆盖所有的点。
易证 存在完美匹配当且仅当 存在偶环覆盖。
- 如果 存在偶环覆盖,我们只需要在每个环都隔一条取一条边,就可以得到一个完美匹配。
- 如果 存在完美匹配,我们只需要将匹配边对应的二元环取出,就可以得到一个偶环覆盖。
然后证明 存在偶环覆盖当且仅当 。
考虑行列式的定义
其中 是任意排列, 表示若 中的逆序对数为奇数,则取 ,否则取 。
不难看出每个排列都可以被看作 的一个环覆盖。如果这个环覆盖中存在奇环,则将这个环翻转后的和一定为 ,因此只有偶环覆盖才能使行列式不为 ,证毕。
定理: 一定为偶数,并且 的最大匹配的大小等于 的一半。
证明
反对称矩阵的秩只能是偶数;后者请读者自行思考。
实际应用中不可能带着 个变量进行计算,不过可以取一个数域,例如取某个素数 的剩余系 ,将变量分别随机替换为 中的数,再进行计算。方便起见,在无歧义的情况下,以下用 直接指代替换后的矩阵。
定理: 至多为 的最大匹配大小的两倍,并且二者相等的概率至少为 。
考虑到一般图最大匹配中 基本不会超过 ,实际中 取 数量级的素数就足够了。
由定理可知,如果只需要求最大匹配数,而无需匹配方案,那么只需要用一次高斯消元求出 即可,远比带花树简洁。不过如果需要输出方案,会稍微复杂一些,需要用到下面介绍的算法。
构造完美匹配
由 Tutte 定理和上面的定理可知,如果 存在完美匹配,那么 有很大概率满秩。方便起见,以下叙述中均省略「有很大概率」。
记 中标号为 的点为 ,进一步地我们有如下定理:
定理: 有完美匹配。
逆矩阵与伴随矩阵
对任意 阶方阵 ,定义其伴随矩阵为 ,其中 为删去第 行第 列的余子式。换言之,设 的代数余子式矩阵为 ,则 。
定理:如果 可逆,那么 。
所以这里的 ,也就是 删去第 行第 列后的部分满秩。
换言之,如果 ,并且 ,就表明存在一个完美匹配方案包含 这条边。以下将这种边称为 可行边。
由如上定理,对于一个有完美匹配的无向图 ,我们可以得到一个比较显然的暴力算法来寻找一组完美匹配:每次枚举 ,如果 是一条可行边(连边存在,并且 ),就将 加入匹配方案,并在 中都删掉这两个点,再重新计算新的 。
总共要做 轮,每轮都是 的,总的复杂度是 ,有点慢了。实际上我们在重新计算 时,不必每次都重新用高斯消元求逆矩阵,而是可以利用如下定理:
定理(消去定理):令
并且 , 那么就有
定理中描述的是消去第一行第一列的情况。实际上,它可以非常显然地推广到消去任意一行一列的情况,因此我们只需在算法最开始计算一次 ,后面每次删除两个点时,只需执行两次 的消去过程即可。
描述有些抽象,可以参考 C++ 代码
void eliminate(int A[][MAXN], int r, int c) { // 消去第 r 行第 c 列 row_marked[r] = col_marked[c] = true; // 已经被消掉 int inv = quick_power(A[r][c], p - 2); // 逆元 for (int i = 1; i <= n; i++) if (!row_marked[i] && A[i][c]) { int tmp = (long long)A[i][c] * inv % p; for (int j = 1; j <= n; j++) if (!col_marked[j] && A[r][j]) A[i][j] = (A[i][j] - (long long)tmp * A[r][j]) % p; } }
总共要做 轮,每轮复杂度为 ,因此上述算法可以在 的时间内找到一组完美匹配。
构造最大匹配
我们刚刚已经解决了构造一组完美匹配的问题,但是求解问题时一般需要最大匹配。
前面已经提到, 的最大匹配大小等于 的一半。如果我们能找到 的一个最大满秩子方阵,那么对子方阵对应的导出子图求出一组完美匹配,即可找到 的一组最大匹配。
换一个角度考虑,如果 有完美匹配,那么 满秩,换言之, 是线性无关的。那么如果 不是满秩的,我们可以求出 的一组线性基,然后只保留线性基对应的行列,就可以得到 的一个最大满秩子方阵。
求出最大满秩子方阵之后,再用上面的算法找出导出子图的一组完美匹配,即可得到原图的一组最大匹配。注意由于高斯消元中可能会有行的交换,因此实现时要注意维护好点的编号。
#include <cstring> #include <iostream> #include <random> #include <utility> using namespace std; constexpr int MAXN = 505, p = (int)1e9 + 7; int qpow(int a, int b) { int ans = 1; while (b) { if (b & 1) ans = (long long)ans * a % p; a = (long long)a * a % p; b >>= 1; } return ans; } int A[MAXN][MAXN], B[MAXN][MAXN], t[MAXN][MAXN], id[MAXN]; // 高斯消元 O(n^3) // 在传入 B 时表示计算逆矩阵, 传入 nullptr 则只需计算矩阵的秩 void Gauss(int A[][MAXN], int B[][MAXN], int n) { if (B) { memset(B, 0, sizeof(t)); for (int i = 1; i <= n; i++) B[i][i] = 1; } for (int i = 1; i <= n; i++) { if (!A[i][i]) { for (int j = i + 1; j <= n; j++) if (A[j][i]) { swap(id[i], id[j]); for (int k = i; k <= n; k++) swap(A[i][k], A[j][k]); if (B) for (int k = 1; k <= n; k++) swap(B[i][k], B[j][k]); break; } if (!A[i][i]) continue; } int inv = qpow(A[i][i], p - 2); for (int j = 1; j <= n; j++) if (i != j && A[j][i]) { int t = (long long)A[j][i] * inv % p; for (int k = i; k <= n; k++) if (A[i][k]) A[j][k] = (A[j][k] - (long long)t * A[i][k]) % p; if (B) { for (int k = 1; k <= n; k++) if (B[i][k]) B[j][k] = (B[j][k] - (long long)t * B[i][k]) % p; } } } if (B) for (int i = 1; i <= n; i++) { int inv = qpow(A[i][i], p - 2); for (int j = 1; j <= n; j++) if (B[i][j]) B[i][j] = (long long)B[i][j] * inv % p; } } bool row_marked[MAXN] = {false}, col_marked[MAXN] = {false}; int sub_n; // 极大满秩子矩阵的大小 // 消去一行一列 O(n^2) void eliminate(int r, int c) { row_marked[r] = col_marked[c] = true; // 已经被消掉 int inv = qpow(B[r][c], p - 2); for (int i = 1; i <= sub_n; i++) if (!row_marked[i] && B[i][c]) { int t = (long long)B[i][c] * inv % p; for (int j = 1; j <= sub_n; j++) if (!col_marked[j] && B[r][j]) B[i][j] = (B[i][j] - (long long)t * B[r][j]) % p; } } int vertices[MAXN], girl[MAXN]; // girl 是匹配点, 用来输出方案 int main() { cin.tie(nullptr)->sync_with_stdio(false); auto rng = mt19937(random_device{}()); int n, m; cin >> n >> m; // 点数和边数 while (m--) { int x, y; cin >> x >> y; A[x][y] = rng() % p; A[y][x] = -A[x][y]; // Tutte 矩阵 } for (int i = 1; i <= n; i++) id[i] = i; // 输出方案用的,因为高斯消元的时候会交换列 memcpy(t, A, sizeof(t)); Gauss(A, nullptr, n); for (int i = 1; i <= n; i++) if (A[id[i]][id[i]]) vertices[++sub_n] = i; // 找出一个极大满秩子矩阵 for (int i = 1; i <= sub_n; i++) for (int j = 1; j <= sub_n; j++) A[i][j] = t[vertices[i]][vertices[j]]; Gauss(A, B, sub_n); for (int i = 1; i <= sub_n; i++) if (!girl[vertices[i]]) for (int j = i + 1; j <= sub_n; j++) if (!girl[vertices[j]] && t[vertices[i]][vertices[j]] && B[j][i]) { // 注意上面那句 if 的写法, 现在 t 是邻接矩阵的备份, // 逆矩阵 j 行 i 列不为 0 当且仅当这条边可行 girl[vertices[i]] = vertices[j]; girl[vertices[j]] = vertices[i]; eliminate(i, j); eliminate(j, i); break; } cout << sub_n / 2 << '\n'; for (int i = 1; i <= n; i++) cout << girl[i] << ' '; return 0; }
习题
参考资料
- Mucha M, Sankowski P.Maximum matchings via Gaussian elimination
- 周子鑫,杨家齐《基于线性代数的一般图匹配》
- ZYQN 《基于线性代数的一般图匹配算法》