零钱兑换问题

1 零钱兑换问题

背包问题是一大类动态规划问题的代表，其拥有很多变种，例如零钱兑换问题。

Question

(给定 $n$ 种硬币，第 $i$ 种硬币的面值为 $coins[i-1]$ ，目标金额为 $amt$ ， 每种硬币可以重复选取 ，问能够凑出目标金额的最少硬币数量。如果无法凑出目标金额，则返回 $-1$ 。示例如图 14-24 所示。)

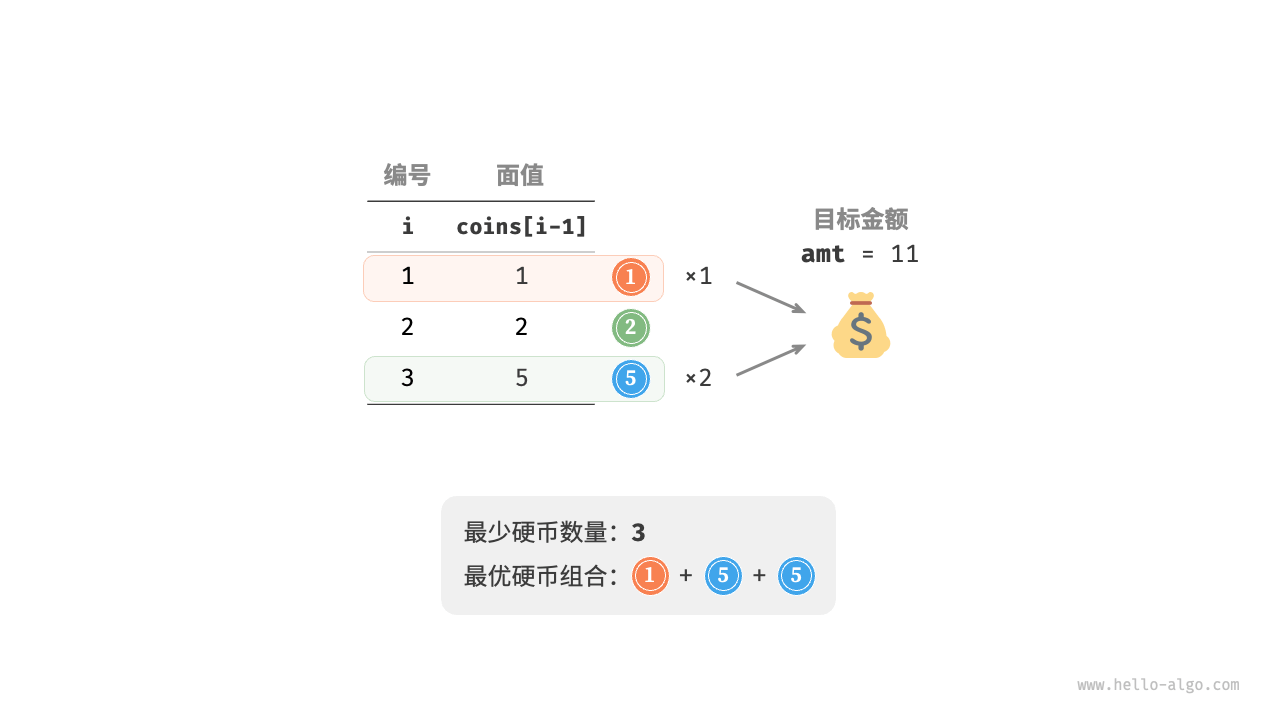
图 14-24 零钱兑换问题的示例数据

1.1 动态规划思路

零钱兑换可以看作完全背包问题的一种特殊情况 ，两者具有以下联系与不同点。

• 两道题可以相互转换，“物品”对应“硬币”、“物品重量”对应“硬币面值”、“背包容量”对应“目标金额”。
• 优化目标相反，完全背包问题是要最大化物品价值，零钱兑换问题是要最小化硬币数量。
• 完全背包问题是求“不超过”背包容量下的解，零钱兑换是求“恰好”凑到目标金额的解。

第一步：思考每轮的决策，定义状态，从而得到 $dp$ 表

状态 $[i,a]$ 对应的子问题为： 前 $i$ 种硬币能够凑出金额 $a$ 的最少硬币数量 ，记为 $dp[i,a]$ 。

二维 $dp$ 表的尺寸为 $(n+1)\times (amt+1)$ 。

第二步：找出最优子结构，进而推导出状态转移方程

本题与完全背包问题的状态转移方程存在以下两点差异。

• 本题要求最小值，因此需将运算符 $max()$ 更改为 $min()$ 。
• 优化主体是硬币数量而非商品价值，因此在选中硬币时执行 $+1$ 即可。

$$dp[i,a]=min(dp[i-1,a],dp[i,a-coins[i-1]]+1)$$

第三步：确定边界条件和状态转移顺序

当目标金额为 $0$ 时，凑出它的最少硬币数量为 $0$ ，即首列所有 $dp[i,0]$ 都等于 $0$ 。

当无硬币时， 无法凑出任意 $>0$ 的目标金额 ，即是无效解。为使状态转移方程中的 $min()$ 函数能够识别并过滤无效解，我们考虑使用 $+\infty$ 来表示它们，即令首行所有 $dp[0,a]$ 都等于 $+\infty$ 。

1.2 代码实现

大多数编程语言并未提供 $+\infty$ 变量，只能使用整型 int 的最大值来代替。而这又会导致大数越界：状态转移方程中的 $+1$ 操作可能发生溢出。

为此，我们采用数字 $amt+1$ 来表示无效解，因为凑出 $amt$ 的硬币数量最多为 $amt$ 。最后返回前，判断 $dp[n,amt]$ 是否等于 $amt+1$ ，若是则返回 $-1$ ，代表无法凑出目标金额。代码如下所示：

/* 零钱兑换：动态规划 */
int coinChangeDP(vector<int> &coins, int amt) {
    int n = coins.size();
    int MAX = amt + 1;
    // 初始化 dp 表
    vector<vector<int>> dp(n + 1, vector<int>(amt + 1, 0));
    // 状态转移：首行首列
    for (int a = 1; a <= amt; a++) {
        dp[0][a] = MAX;
    }
    // 状态转移：其余行和列
    for (int i = 1; i <= n; i++) {
        for (int a = 1; a <= amt; a++) {
            if (coins[i - 1] > a) {
                // 若超过目标金额，则不选硬币 i
                dp[i][a] = dp[i - 1][a];
            } else {
                // 不选和选硬币 i 这两种方案的较小值
                dp[i][a] = min(dp[i - 1][a], dp[i][a - coins[i - 1]] + 1);
            }
        }
    }
    return dp[n][amt] != MAX ? dp[n][amt] : -1;
}

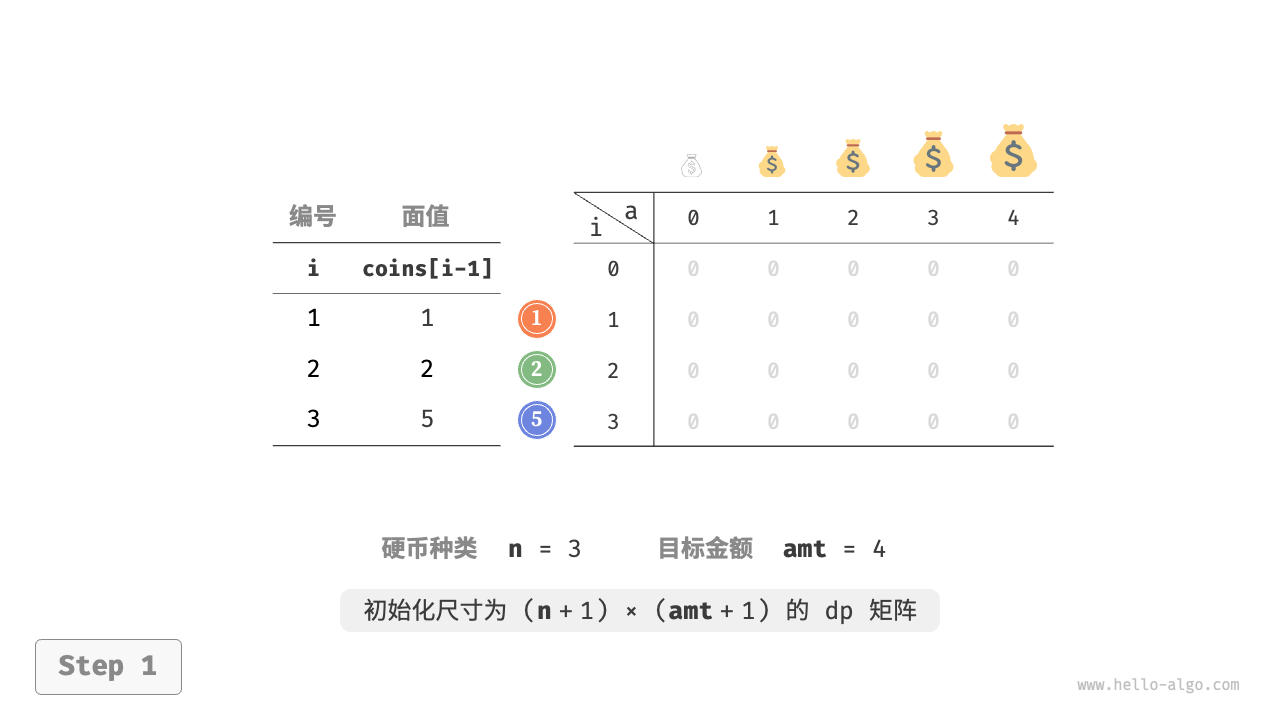
图 14-25 展示了零钱兑换的动态规划过程，和完全背包问题非常相似。

图 14-25 零钱兑换问题的动态规划过程

1.3 空间优化

零钱兑换的空间优化的处理方式和完全背包问题一致：

/* 零钱兑换：空间优化后的动态规划 */
int coinChangeDPComp(vector<int> &coins, int amt) {
    int n = coins.size();
    int MAX = amt + 1;
    // 初始化 dp 表
    vector<int> dp(amt + 1, MAX);
    dp[0] = 0;
    // 状态转移
    for (int i = 1; i <= n; i++) {
        for (int a = 1; a <= amt; a++) {
            if (coins[i - 1] > a) {
                // 若超过目标金额，则不选硬币 i
                dp[a] = dp[a];
            } else {
                // 不选和选硬币 i 这两种方案的较小值
                dp[a] = min(dp[a], dp[a - coins[i - 1]] + 1);
            }
        }
    }
    return dp[amt] != MAX ? dp[amt] : -1;
}

2 零钱兑换问题 II

Question

(给定 $n$ 种硬币，第 $i$ 种硬币的面值为 $coins[i-1]$ ，目标金额为 $amt$ ，每种硬币可以重复选取， 问凑出目标金额的硬币组合数量 。示例如图 14-26 所示。)

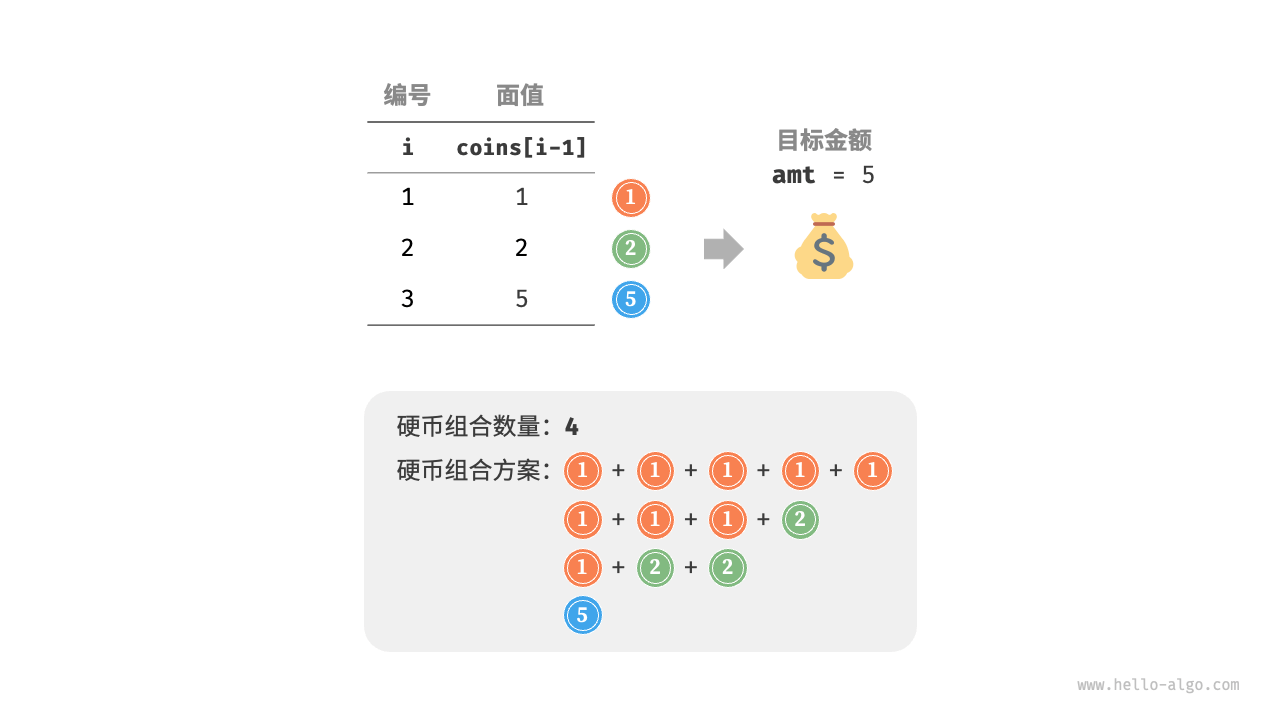
图 14-26 零钱兑换问题 II 的示例数据

2.1 动态规划思路

相比于上一题，本题目标是求组合数量，因此子问题变为： 前 $i$ 种硬币能够凑出金额 $a$ 的组合数量 。而 $dp$ 表仍然是尺寸为 $(n+1)\times (amt+1)$ 的二维矩阵。

当前状态的组合数量等于不选当前硬币与选当前硬币这两种决策的组合数量之和。状态转移方程为：

$$dp[i,a]=dp[i-1,a]+dp[i,a-coins[i-1]]$$

当目标金额为 $0$ 时，无须选择任何硬币即可凑出目标金额，因此应将首列所有 $dp[i,0]$ 都初始化为 $1$ 。当无硬币时，无法凑出任何 $>0$ 的目标金额，因此首行所有 $dp[0,a]$ 都等于 $0$ 。

2.2 代码实现

/** 背包问题变种：零钱兑换II TC: O(N*A), SC: O(A) */
int coinChangeII(vector<int>& coins, int A) {
    int N = coins.size();
    vector<int> dp(A + 1, 0);
    dp[0] = 1; // 目标金额为0只有一种组合方式：空集
    for (int i = 1; i <= N; i++) {
        int coin = coins[i - 1];
        for (int j = 1; j <= A; j++) {
            if (coin <= j) {
                // 不选新硬币的方案 dp[j], 选新硬币的方案 dp[j-coin]
                dp[j] = dp[j] + dp[j - coin];
            } else {
                // 新硬币比目标金额大，肯定用不到
                // dp[j] = dp[j];
            }
        }
    }
    return dp[A];
}

这里必须解释下 dp 循环中关键的一句：

dp[j] = dp[j] + dp[j - coin];

因为这里 dp 内循环是正向的，这意味着 dp[j-1],dp[j-2],...,dp[j-coin],...,dp[0] 已经是当前轮的状态，而 等式右边的 dp[j] 还是上一轮的状态，如果按包含当前硬币的数量来给右边 dp[j] 和 dp[j-coin] 的方案分类的话：

• 右边 dp[j] 的方案包含：包含当前硬币数为 0、总金额为 j 的全部方案
• dp[j-coin] 的方案包含：包含当前硬币数为 (0,1,2,…)、总金额为 j-coin 的全部方案
  • 将 dp[j-coin] 的方案都加一个当前的硬币后，变成了包含当前硬币数为 (1,2,3,…)、总金额为 j 的全部方案。 所以两者加起来就是包含当前硬币数为 (0,1,2,…)、总金额为 j 的全部方案，也即本轮外循环中 dp[j] 的含义。

零钱兑换 III

Question

给你 $100,$50, $20,$10, $5的纸钞和$2, $1, 50c, 20c, 10c, 5c 的硬币。给你某金额的数字，问有多少种不同的方法可以组合成这个金额。

零钱兑换的变种，不过涉及浮点数，这里可以都乘以 100 转成整数来处理。