树上背包是树形 dp 的常见模型,通常是分组背包的变形,而分组背包的本质就是多个泛化物品不断相加。因此掌握泛化物品的合并的方法有助于理解转移的过程(具体见 1.4)。 此类问题一般也可以用 DFS 序、多叉转二叉等方法解决。
1 引入:二叉苹果树
P2015 二叉苹果树 题意简述:在一个二叉树中,每个边有一个权值。我们要保留 条边组成的连通分量(必须包含根节点),求边权和最大值。
我们思考,从节点 (根节点)开始保留 条边,最大答案是什么?
我们分出 种情况,根节点的答案就是这 种情况的最大值:
- 保留连接左子结点的边。这种情况下我们消耗 条边连接左子结点,那么从根节点开始保留 条边,就相当于从左子结点开始保留 条边的答案。
- 保留连接右子节点的边。同上,相当于从右子结点开始保留 条边的答案。
- 左右都保留。连接左右消耗 条边,剩下 条边,我们需要循环枚举分给左边多少,右边多少。
用 表示以 为根的子树,保留 条边的最大答案。 实现细节:因为题目输入边的方向不定,所以我们双向存图,并且使用 数组。
代码
/* 二叉苹果树 https://www.luogu.com.cn/problem/P2015 */ #include <algorithm> #include <iostream> #include <vector> using namespace std; struct edge { int to, w; // to: 连接的节点,w: 这条边上的苹果数 }; vector<edge> G[110]; // 邻接表存储树 int f[110][110], n, q; // f[i][j]: 以i为根的子树中保留j条边能获得的最大苹果数 bool vis[110]; /* TC: O(N × Q²) SC: O(N × Q) */ void dfs(int pos) { if (G[pos].size() == 1) { return; } int ch[2], w[2], len = 0; for (auto i : G[pos]) { if (!vis[i.to]) { w[len] = i.w; // 记录到子节点的边权(苹果数) ch[len++] = i.to; // 记录子节点 } } vis[pos] = 1; // 标记当前节点已访问 dfs(ch[0]); dfs(ch[1]); for (int i = 1; i <= q; i++) { // 情况1:只选择一个子树 f[pos][i] = max(f[ch[1]][i - 1] + w[1], f[ch[0]][i - 1] + w[0]); // 情况2:两个子树都选择 for (int j = 0; j <= i - 2; j++) { f[pos][i] = max(f[pos][i], f[ch[0]][j] + w[0] + f[ch[1]][i - j - 2] + w[1]); } } vis[pos] = 0; } int main() { cin >> n >> q; for (int i = 1; i < n; i++) { int u, v; edge e; cin >> u >> v >> e.w; e.to = v, G[u].emplace_back(e); e.to = u, G[v].emplace_back(e); } dfs(1); cout << f[1][q]; return 0; }
1.1 分组背包
树形 DP + 分组背包解法思路:
- 表示以 为根的子树中,保留 条边的最大苹果数
- 对于每个子树,将其看作一个物品组,使用分组背包的思路合并
代码
/* 二叉苹果树 https://www.luogu.com.cn/problem/P2015 */ #include <vector> using namespace std; struct Node { int parent; // -1 表示根节点 vector<int> sons; int value; // 表示该节点与其父节点之间的边的苹果数 }; // 树形DP + 分组背包解法 // f[u][i] 表示以 u 为根的子树中,保留 i 条边的最大苹果数 // 对于每个子树,将其看作一个物品组,使用分组背包的思路合并 void dfs(int u, const vector<Node>& nodes, int Q, vector<vector<int>>& f) { auto& root = nodes[u]; if (root.sons.empty()) { return; } // 对每个子节点,使用分组背包合并 for (int s : root.sons) { dfs(s, nodes, Q, f); // 先递归处理子树 // 倒序遍历,类似01背包,避免重复使用同一子树 for (int i = Q; i >= 1; i--) { // 枚举分配给子树 s 的边数 j (包括连接边) for (int j = 1; j <= i; j++) { // f[u][i-j]: 不分配给s或分配较少边的最优状态 // f[s][j-1]: 子树s内部选j-1条边的最大值 // nodes[s].value: 连接u到s的边的苹果数 f[u][i] = max(f[u][i], f[u][i - j] + f[s][j - 1] + nodes[s].value); } } } } int binaryAppleTree(const vector<Node>& nodes, int Q) { // f[u][i] 表示以 u 为根节点的子树中保留 i 条边的最大苹果数 vector<vector<int>> f(nodes.size(), vector<int>(Q + 1, 0)); // 假定第一个node就是根节点 dfs(0, nodes, Q, f); return f[0][Q]; }
2 例 1:选课问题
Note
P2014 [CTSC1997] 选课 题意简述:在大学,有 门课来学习,每个课程有一个先修课,或者没有(要学习某门课,必须先学习它的先修课)。学一门课可以得到相应的学分。请问学 门课,最多能得多少学分。
因为给定的图是一片森林,不好操作,我们把所有无先修课的课程,都设置上一个公共的先修课——节点 。这样变成树后就好操作了。注意相应地, 需要 。
我们再回到这个题,与上一道题最大的不同点就在于——不是二叉树了。
回想上一题,如果是二叉树,我们可以枚举从这一节点开始保留的 门课,分给左右子结点各多少门。但现在这不是二叉树了,我们该怎么考虑呢?
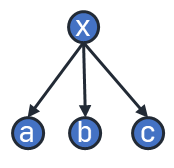
如上图, 的前驱都是 。我们设正在求从 开始学习 门课的最大学分。
我们受上一道题的影响,考虑枚举每个子节点分配多少。 (虽然上一题是边,这一题是点,但考虑方式相似) 首先根节点必须选,自己用去 后,子节点还能用 个。 但我们仔细思考,会发现这是一个对 分拆成多个个自然数之和的问题。我们需要枚举每个子节点分配多少,效率上就已经输了 (TC 为 , n 为子节点个数)。所以我们考虑使用背包。
2.1 分组背包
受上一题的启发,我们用 表示以 为根的子树,学 门课的最大学分。 对于 的每个子节点,我们可以对其分配 门课( 是该子树的大小)。
我们发现这是一个泛化物品的背包问题(每个物品随着你给它分配的空间而改变为不同的价值。这里每个子节点相当于物品,给其中一个物品 分配 个物品,各自的价值就是 )。
这类问题,我们常常可以将其转化为分组背包问题(物品分组,每组内物品最多选 个的背包问题,具体见 此文 )。因为我们发现,其实 一个泛化物品就是一个“组” 。
背包容量为 ,每个子节点 都是一组,每组内有 个元素,组内第 个元素重量为 ,价值为 。
注意 :根节点 必须要选,所以搜索之前我们需要赋初值 。
虽然我们的状态表示是 ,但是 表示的是根节点编号,和背包没有任何关系,不要被迷惑了。真正起作用的只有 而已。所以用于背包的其实只有一维,这是一个空间压缩为一维的分组背包。
附上一维分组背包 Code,注意第 层的倒序枚举:
for(int i=1;i<=s;i++){
for(int k=m;k>=1;k--){
for(int j=1;j<=n[i];j++){
if(k>=w[i][j]) f[k]=max(f[k],f[k-w[i][j]]+v[i][j]);
}
}
}最终求出的答案是 ,注意这里的 已经加过 了。
#include<bits/stdc++.h>
using namespace std;
int n,m;
vector<int> G[1010];
int f[1010][1010];
void dfs(int pos){
for(auto i:G[pos]){
dfs(i);
for(int j=m;j>1;j--){
for(int k=1;k<j;k++){
f[pos][j]=max(f[pos][j],f[pos][j-k]+f[i][k]);
}
}
}
}
int main(){
cin>>n>>m;
m++;
for(int i=1;i<=n;i++){
int u;
cin>>u>>f[i][1];
G[u].emplace_back(i);
}
dfs(0);
cout<<f[0][m];
return 0;
}2.1.1 上下界优化
我们发现这份代码只是一个雏形,其实还有许多地方可供优化。上文我们提到了边界 的问题。故我们用 表示“当前遍历过的子树大小(包括 )”,在搜索的过程中实时累加,便可以得到以下优化(建议结合代码理解):
- 枚举 (给子节点 分配的个数)只需从 开始,枚举到 即可。 其原因就是:以 的子节点 为根的子树最多只有 个节点,超出就没有遍历的必要性了,同样地,如果 ,则分给已合并部分的个数就 ,同样没必要考虑。
- 相应地,既然超过子树大小就调用不到了,我们还额外求它有什么用呢? 所以, 枚举 (背包大小)只需要从 开始。
#include<bits/stdc++.h>
using namespace std;
int n,m;
vector<int> G[1010];
int f[1010][1010],siz[1010];
void dfs(int pos){
siz[pos]=1;
for(auto i:G[pos]){
dfs(i);
for(int j=min(m,siz[pos]+siz[i]);j>1;j--){
//j>siz[pos]+siz[i]就没有计算的必要了,
//因为根本调用不到这个值
int lim=min(j-1,siz[i]);
//k之所以要<=siz[i]是因为下面调用了f[i][k],
//如果k>siz[i]是没有必要遍历的
for(int k=max(1,j-siz[pos]);k<=lim;k++){
//k之所以从j-siz[pos]开始是因为下面调用了f[pos][j-k],
//而如果j-k>siz[pos]是没有必要遍历的
f[pos][j]=max(f[pos][j],f[pos][j-k]+f[i][k]);
}
}
siz[pos]+=siz[i];
//注意这里siz[pos]是实时累加的
}
}
int main(){
cin>>n>>m;
m++;
for(int i=1;i<=n;i++){
int u;
cin>>u>>f[i][1];
G[u].emplace_back(i);
}
dfs(0);
cout<<f[0][m];
return 0;
}这个优化十分重要, 情况下,可以把时间从 100ms 左右降到 10ms 以内。
理解起来可能有一定难度,建议自己造一个样例模拟填表的过程,多填几遍。下图可能会给你帮助:
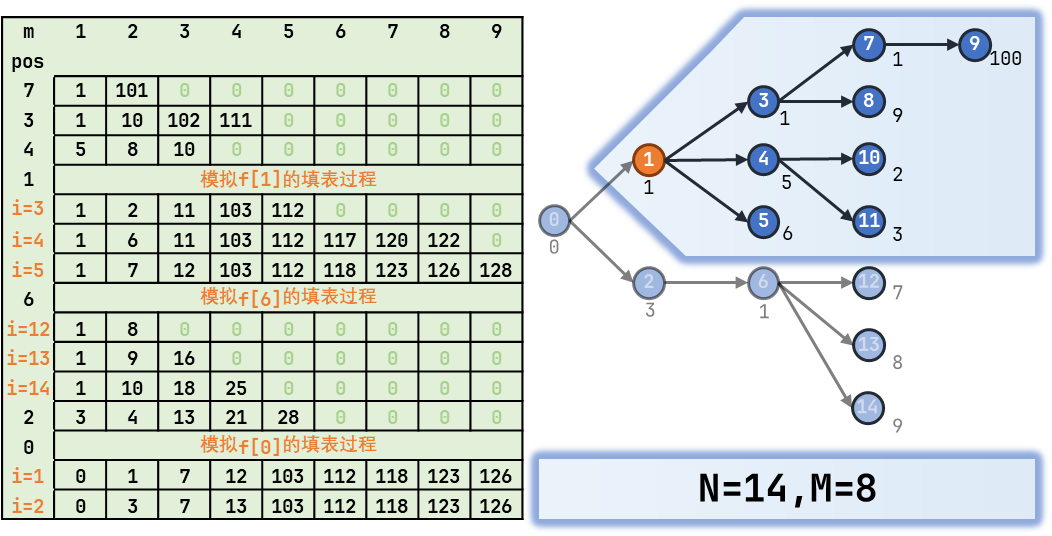
附上图中样例:
Sample
14 8
0 1
0 3
1 1
1 5
1 6
2 1
3 1
3 9
7 100
4 2
4 3
6 7
6 8
6 9U53204 【数据加强版】选课
这道加强版数据范围是 , 。
因此用这种方法做需要注意用 vector ,根据 的大小动态开数组,才不会 MLE。
1.1 分组背包上下界优化
#include<bits/stdc++.h>
using namespace std;
int n,m;
vector<int> G[1010],f[1010];
int siz[1010],v[1010];
void dfs(int pos){
f[pos].resize(m+1);
//其实根据上下界优化,有些情况不用开到m
//但是此时该节点的大小还没计算出来
//如果提前计算代码就得翻新了(懒)
f[pos][1]=v[pos];
siz[pos]=1;
for(auto i:G[pos]){
dfs(i);
for(int j=min(m,siz[pos]+siz[i]);j>1;j--){
int lim=min(j-1,siz[i]);
for(int k=max(1,j-siz[pos]);k<=lim;k++){
f[pos][j]=max(f[pos][j],f[pos][j-k]+f[i][k]);
}
}
siz[pos]+=siz[i];
}
}
int main(){
cin>>n>>m;
m++;
for(int i=1;i<=n;i++){
int u;
cin>>u>>v[i];
G[u].emplace_back(i);
}
dfs(0);
cout<<f[0][m];
return 0;
}2.1.2 复杂度分析
我们简单分析一下算法的复杂度。
空间的话,就是 。
而时间,我们先考虑朴素算法,每个节点都遍历自己的子节点 遍,共 ;对于每个子节点,枚举背包大小,共 ;对于每个背包大小我们枚举 ,共 。所以时间复杂度上界是 。
上下界优化后的时间复杂度是 ,下面我们进行证明。
内容转述自 ouuan 的 「树上背包的上下界优化」 ,万分感谢原作者!!
2.1.3 A - 证明
我们先思考,如果没有 的限制,合并以 为根节点的子树,时间复杂度是多少?
设 处理以 为根的子树的时间,那么
解释: 计算 时,对于第 步得到的式子,我们显然可以把 都去掉。接下来我们利用放缩,把原式扩大成 ,接下来运用乘法分配律,就得到 的上界 了。
对于所有叶子节点 , 。
那么对于计算 中的 ,每个 的上界都是 ,而平方的和一定 和的平方,所以 上界是 ,又因为 也是 ,所以 。故初步时间复杂度是 。
接下来,我们思考有 的限制时,时间复杂度将会是多少。
此时,因为要和 取最小值,所以
与上面相似地,叶节点 的 是 。
每个 的上界都是 ,加起来, 上界是 ,又因为 ,所以更精确的时间复杂度是 。
呜哇 树形 dp 水好深 (・・)
2.2 DFS 序解法
我们把树上的节点按 DFS 序编号:
 那么,我们用 表示编号为 的节点 (按后序遍历的顺序) 中,选 个节点,所能获得的最大学分。
用 表示 DFS 序中第 个是什么。
那么,我们用 表示编号为 的节点 (按后序遍历的顺序) 中,选 个节点,所能获得的最大学分。
用 表示 DFS 序中第 个是什么。
那么对于 个点,我们分两种情况讨论:
- 选当前点。 那么,该点的子树中,所有点都可以参与考虑。 。
- 不选当前点。 那么,该点的子树都不能参与考虑。此时需要退回到该节点为根的子树以外。因为是后序遍历,所以节点 为根的子树前,最晚遍历的点就是 。故 。
两种情况取最大即可。
时空复杂度显然都是 。
实现细节的话,还是请注意 vector 需要动态开大小。否则会 MLE。
1.2 - DFS 序
#include<bits/stdc++.h>
using namespace std;
int n,m,v[100010];
vector<int> G[100010],f[100010];
int siz[100010],awa[100010],len;
void dfs(int pos){
siz[pos]=1;
for(auto i:G[pos]){
dfs(i);
siz[pos]+=siz[i];
}
awa[++len]=pos;
}
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
int u;
cin>>u>>v[i];
G[u].emplace_back(i);
}
dfs(0);
f[0].resize(m+1);
for(int i=1;i<=n;i++){
f[i].resize(m+1);
for(int j=1;j<=m;j++){
f[i][j]=max(f[i-1][j-1]+v[awa[i]],f[i-siz[awa[i]]][j]);
}
}
cout<<f[n][m];
return 0;
}2.3 多叉转二叉解法
收到“二叉苹果树”的启发,我们发现如果能把多叉树转化成二叉树,那么转移时仅需枚举左子结点分配个数即可,十分方便。但是我们怎么将多叉转为二叉呢?
具体方法就是不断递归,找到根节点,把它与最左边的子节点之间的边保留,其他全部断掉。然后从这个保留的孩子开始,连一条链到所有断开的点。 具体见此文 。
用上面的例子,转完二叉数的图如下。
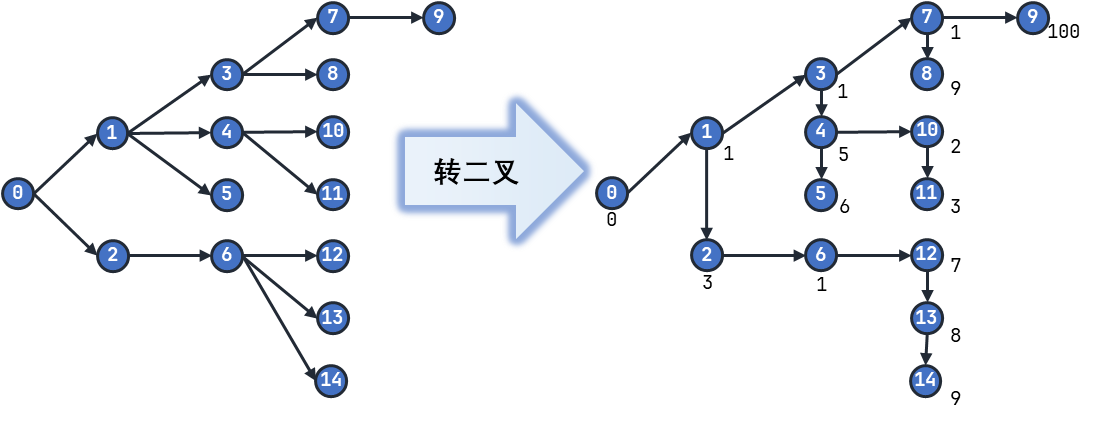
注意:此二叉树区分左右孩子,我们把保留的最左边的节点作为根的 左子节点 ,链上的点都是其父节点的 右子节点 。
根据上面的规则,我们对上图进行整理,使左右子节点关系更清晰。
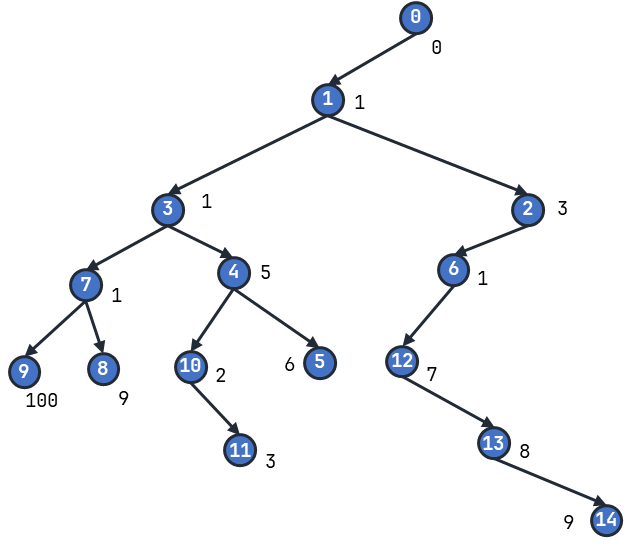
注意到对于节点 ,其左子节点就是原图中的 最左边的子节点,而右子节点就是原图中的 的兄弟。于是转移时,我们先一层大循环枚举 ,即节点 有多少门课可以学。接下来,我们分类讨论:
- 根节点自己用去 个。那么还剩下 门课可以学,我们枚举这 门课在左右子节点之间的分配即可,和引入的思路相同。
- 根节点自己不用。这里和引入有些不一样了,根节点可以不选。这是因为 的右子节点在 原图中 是自己的兄弟,也就是说,如果我们不选根节点 ,不影响我们选它的右子节点(也就是原图中的兄弟节点)。我们需要让“根节点不选,其他 门课全给右子节点”的状态参与考虑。
两种情况取最大即可。
但是我们注意到,引入部分代码的的时间复杂度是 ,会超时。
于是我们受 1.1.2 中树上背包优化的启发,对上下界进行优化。
把枚举和计算范围都限制在 以内即可。
易证时间复杂度是 ,因为每个节点花费上限 去平衡左右子树,一共 个节点。
详见代码注释。
1.3 - 多叉转二叉
#include<bits/stdc++.h>
#define NO 100009
using namespace std;
int n,m,v[100010],lc[100010],rc[100010];
int siz[100010];
vector<int> G[100010],f[100010];
void dfs(int pos){
if(pos==NO) return;
dfs(lc[pos]);
dfs(rc[pos]);
for(int i=1;i<=min(m,siz[pos]);i++){
f[pos][i]=f[rc[pos]][i];
//不需要 ...][i] => ...][min(i,siz[rc[pos]])]
//原因是如果i>siz[rc[pos]],就说明把右节点分配满,
//也有剩余的课程可以加到pos和pos的左子节点
//这个语句就相当于没用了
int lj,rj;
rj=min(i-1,siz[lc[pos]]);
//左节点最多分配siz[lc[pos]]个
lj=max(0,i-1-siz[rc[pos]]);
//右节点最多分配siz[rc[pos]]个
//而右节点个数是i-1-j,
//所以j最大枚举到i-1-siz[rc[pos]]
for(int j=lj;j<=rj;j++){
//左 j个 右 i-1-j个
int l=f[lc[pos]][j];
int r=f[rc[pos]][i-1-j];
f[pos][i]=max(f[pos][i],l+r+v[pos]);
}
}
}
void conv(int pos){
siz[pos]=1;
int prei=-1;
for(auto i:G[pos]){
if(prei==-1) lc[pos]=i;
else rc[prei]=i;
prei=i;
conv(i);
}
}
void cntsiz(int pos){
if(pos==NO) return;
cntsiz(lc[pos]);
cntsiz(rc[pos]);
siz[pos]=1+siz[lc[pos]]+siz[rc[pos]];
}
int main(){
cin>>n>>m;
m++;
for(int i=1;i<=n;i++){
int u;
cin>>u>>v[i];
G[u].emplace_back(i);
}
for(int i=0;i<=n;i++) f[i].resize(m+1),lc[i]=rc[i]=NO;
f[NO].resize(m+1);
conv(0);//转二叉
cntsiz(0);//计算大小
dfs(0);
cout<<f[0][m];
return 0;
}2.4 泛化物品求并解法
来源: 徐持衡 - 国家集训队2009论文集 浅谈几类背包题 。
设 为遍历到节点 ,从已遍历的点中选择 个节点而且 必须选择 的答案。
每一个 都是一个泛化的物品。给 分配 的空间,获得的价值就是 。
我们假设当前遍历到 ,现在需要处理 的一个子节点 。
因为 的前驱是 ,所以 初值为 。
假设现在完成了对 的处理,那么现在对于两个物品 和 , 表示选 不选 的答案, 表示选 也选 的答案。两者一同覆盖了“选 ”这一条件,所以在合并的时候我们需要对每个大小下的价值取 ,即对子节点和合并到现在的根节点进行一个“泛化物品的并”运算。
在这里需要明确 个概念、求法、复杂度和它们的适用情况:
-
两个泛化物品的和: 两个泛化物品 ,分配大小为 时价值分别为 。它们的和为泛化物品 ,那么 表示 的大小,可以随意分配给 能获得的最大价值。
- 求法: ( 表示可取大小的最大值)。
- 复杂度: ,每个大小遍历一次,共 ;每次枚举 又花费 。
- 适用情况: 可以在两个物品之间进行分配。 绝大多数树上的背包都是这种做法。比如 1.1.1 的分组背包就是一个不断求两个泛化物品之和的过程,每次将子节点和之前遍历过的子树进行合并。每个点都要完成一个 的合并,时间复杂度就是 ,优化上下界后才变成 。
-
泛化物品与普通物品的和: 一个泛化物品 和一个普通物品 , 的大小为 ,价值为 ,泛化物品 。
-
求法:
-
复杂度: 。
-
适用情况:比如 01 背包、完全背包这些问题,它们本质上就是不断把普通物品加到泛化物品中,一共加 次(所以时间复杂度 )。
-
-
两个泛化物品的并: 两个泛化物品 ,它们的并为 。
- 求法: 。
- 复杂度 。
- 适用情况: 两个物品只能取一个。 比如当前这种解法, 与 一同覆盖了“选 ”这一条件,因此合并时不能求和,而是求并。 1.4 - 泛化物品求并
#include <algorithm>
#include <iostream>
#include <vector>
using namespace std;
int n, m, v[100010];
vector<int> G[100010], f[100010];
void dfs(int u, int dep) {
for (auto s : G[u]) {
for (int j = dep + 1; j <= m; j++) {
f[s][j] = f[u][j - 1] + v[s];
}
dfs(s, dep + 1);
for (int j = dep + 1; j <= m; j++) {
f[u][j] = max(f[u][j], f[s][j]);
}
}
}
int main() {
cin >> n >> m;
for (int i = 1; i <= n; i++) {
int u;
cin >> u >> v[i];
G[u].emplace_back(i);
}
for (int i = 0; i <= n; i++) {
f[i].resize(m + 1);
}
dfs(0, 0);
cout << f[0][m];
return 0;
}Note
理解这个解法的核心是要理解 的含义, 这个解法里 表示遍历到当前节点 u 时选节点 u 以及从其他已遍历的节点中选 j-1 个节点的解. 这里有几点需要注意:
- dfs 遍历是个有来有回的过程, 最开始从虚拟根节点出发, 来来回回逐个子节点 dfs 遍历,最后回到虚拟根节点, 因此当前已遍历节点这个集合是不断在变化的, 所以 也需要不断更新, 不可能一次遍历就完成所有的更新.
- 选的节点都是真节点, 不包括虚拟根节点 (因为 dep 从 0 开始)
- j -1 个节点中一定包含虚拟根节点到 u 的路径上的节点 (不然也遍历不到 u)
回到 dfs(u, dep) 的过程, 当循环到其子节点 s 时,
f[s][j] = f[u][j - 1] + v[s];的含义是: 遍历 s 节点, 设当前已遍历节点集合为 , 则 表示接下来遍历到 s, 选 s 及从 中选 个节点的解, 注意从虚拟根节点到 s 路径上的点 (包含 u) 是在这 j-1 个节点中的, 剩下的节点则是从 N_u 中 u 的其他已遍历的子树中的节点选的.dfs(s, dep + 1);递归遍历 s 子树,直至遍历完其所有子节点,最后回到 u. 经过这一步后, 已遍历的点集为 , 其中 是 s 子树所有点 (含 s), 此时 中的点对应的 f 是已经更新好的状态, 符合其定义.f[u][j] = max(f[u][j], f[s][j]);因为前面遍历了 s 子树的所有节点 ,已遍历的点集变为 , 而 的状态还停留在已遍历点集为 的状态, 所以需要更新 的状态, 因为如果不选 s, 则 s 子树所有的点也不能选, 因此现在的 可以认为是从已遍历的点集 中选 u 不选 s 共选 j 个节点的解, 而 则是从已遍历的点集 中选 u 选 s 共选 j 个节点的解, 两种情况不可能同时发生, 只能取其一, 因此 便是从已遍历的点集 中选 u 共选 j 个节点的解, 符合定义, 即 的状态得到了更新.- 至此完成了对子节点 s 的处理, 回到 u, 继续处理 u 的其他子节点, 等处理完所有子节点, 的含义就变成了从已遍历的点集 中选 u 共选 j 个节点的解, 特别的,当节点 u 为虚拟根节点时, 最后的含义就是从所有真节点 (不含虚拟节点) 中选 j 个节点的解, 也就是最终的答案.
2.5 总结
这 种方法时间复杂度都为 ,跑加强版都能保持在所有测试点 左右。主要是还没有进行常数优化,比如 I/O 等等。
其中我们最常用的是第 种,不过多了解一些算法总归没有坏处嘛。
最后总结的这三个概念,个人感觉是背包 中很本质的东西。结合一下适用情况就可以发现,背包转移几乎都可以用这三个求法来概括。如果从这一角度来解释转移,就会变得很好理解。
3 例 2:有线电视网
给定一个树形结构。其中根节点是足球比赛的现场,叶子节点是用户终端,其他节点就是转播站。每条边都有一个边权,表示信号传递的消费。每个叶子都有一个点权,表示每个用户准备的钱数。
请问在不亏本的情况下,最多能让多少用户看到比赛? (注意不是让赚的钱最多)
此题我们用分组背包来实现。用 表示以 为根,让 个观众看到比赛的最大收益。用 表示以 为根的子树中有多少个叶子。
与上面 1.1.2 的代码十分相像了,同样是 两个泛化物品求和 ,具体见代码吧。只不过有以下细节需要注意:
- 由于各子树选择叶子节点,不存在对父节点的依赖关系,所以 需要枚举到 ,相应地 也需要枚举到 。
- 的初始值应为极小值,因为收益可能为负。特别地, 。
- 因为此题中遍历每一条边也有相应的花费,所以泛化物品的价值需要减去边权。
- 题目不是让赚的钱最多,所以我们是要从大到小遍历 , 非负则输出 ,结束程序。
时间复杂度与树上背包相同,是 。
2 点击查看代码
#include<bits/stdc++.h>
using namespace std;
struct edge{int to,w;};
vector<edge> G[3010];
int n,m,v[3010];
int f[3010][3010],siz[3010];
//siz[i]表示i为根的子树,叶子的个数
//f[i][j]表示i为根,让j个观众看到的最大收益
void dfs(int pos){
if(pos>n-m){
f[pos][1]=v[pos];
siz[pos]=1;
}
for(auto i:G[pos]){
dfs(i.to);
siz[pos]+=siz[i.to];
for(int j=siz[pos];j>=1;j--){
for(int k=1,lim=min(siz[i.to],j);k<=lim;k++){
f[pos][j]=max(f[pos][j],f[pos][j-k]+f[i.to][k]-i.w);
}
}
}
}
int main(){
cin>>n>>m;
memset(f,128,sizeof f);//int极小值
for(int i=1;i<=n;i++) f[i][0]=0;
for(int i=1;i<=n-m;i++){
int k;
edge tmp;
cin>>k;
for(int j=1;j<=k;j++){
cin>>tmp.to>>tmp.w;
G[i].emplace_back(tmp);
}
}
for(int i=n-m+1;i<=n;i++) cin>>v[i];
dfs(1);
for(int i=m;i>=0;i--){
if(f[1][i]>=0){
cout<<i;
break;
}
}
return 0;
}4 例 3:重建道路
有一个 个节点的树形结构,现在要剪断若干条边,使得产生一个大小恰好为 的连通块。请问最少需要剪断多少条边?
我们简单地设 表示以 为根节点的子树中,保留大小为 的子树连接父节点的最小删边次数。
设当前在处理以 为根的子树,需要保留 个节点。
由于保留的子树需要与父节点联通,所以显然根节点 必须要选,子孙结点中一共要保留 个。
我们就发现这是一个泛化物品的背包问题了。每个 都是一个泛化的物品,如果给这个物品分配 的空间,所获得的价值是 。现在对于总空间 ,要让价值和最小(即让删边次数最小)。
我们对于每一个子节点,将其合并到根节点上来。相当于 两个泛化物品求和 (上面有提到)的过程。
转移: 枚举的是 的所有子节点 枚举的是 ,即保留的节点个数 枚举的是分给子节点多少个( 不能 的原因就是根节点必须选,子节点最多选 ,上面说了)
很好理解,要么前面合并的子树已经保留 个节点了,当前这个子节点 根本不需要,于是把 和当前子节点 之间的边断掉,额外 ;要么考虑给当前节点分配多少个, 。
枚举的上下界优化和 1.1.2 类似,不再赘述。
最终答案是 。 除了 其他都需要额外 的原因是需要额外断掉根节点和它父节点之间的连边。
关于初始化:因为取最小值所以全部设为正无穷。但要注意不要置为最大值,因为代码中有 的过程,如果置为最大可能会溢出。特别地, ,因为一开始一个子节点都没遍历,所以一开始就满足“保留 个点”。
时间复杂度 ,证明同分组背包。
3 点击查看代码
#include<bits/stdc++.h>
using namespace std;
int n,P,siz[160];
int f[160][160],ans;
vector<int> G[160];
void dfs(int pos){
siz[pos]=1,f[pos][1]=0;
for(auto i:G[pos]){
dfs(i);
for(int j=min(P,siz[pos]+siz[i]);j>=1;j--){
f[pos][j]++;//注意需要放在外面
for(int k=max(1,j-siz[pos]);k<=min(siz[i],j-1);k++){
f[pos][j]=min(f[pos][j],f[pos][j-k]+f[i][k]);
}
}
siz[pos]+=siz[i];
}
}
int main(){
cin>>n>>P;
memset(f,127,sizeof f);//int极大值
for(int i=1;i<n;i++){
int u,v;
cin>>u>>v;
G[u].emplace_back(v);
}
dfs(1);
ans=f[1][P];
for(int i=2;i<=n;i++) ans=min(ans,f[i][P]+1);
cout<<ans;
return 0;
}5 例 4:软件安装
有 个软件,每个软件有一个依赖软件,或没有。如果有依赖软件,则必须先安装依赖软件,才能运行此软件。软件 占空间 ,如果该软件能运行,则会产生 的价值。给定磁盘空间 ,请问价值最大是多少?
首先我们需要意识到这道题可能是有环的,给定的图是一个 基环树森林 。遇到这种情况我们可以将环缩为一个点,这个点的 是环上所有点的 求和, 也是环上所有点的 之和。因为对于一个环,我们要么都安装,要么都不安装。
这里使用 Tarjan 求强连通分量来缩点,其实直接拓扑排序/dfs 找环也可以。 如果没学过 Tarjan 可以阅读 我的文章 ,或者观看 [算法]轻松掌握tarjan强连通分量 (P4 开始看就可以)。
缩点后就是一片森林了。和选课相同,我们把所有入度为 的节点添上 个公共父节点——节点 。
接下来就和选课很相像了。但选课限制的是选择节点的个数,这道题限制的是选择节点占的空间。
我们回顾一下分组背包的代码:
- 初始化: ; 修改后: 对于 , ;
- : 不修改
- : (倒序) 修改后: (倒序)
- : 修改后:
其实就是把 都变成了 ,然后初始化相应地改一下就行。如果理解了上下界优化,这个应该比较好懂。
void dfs(int pos){
int tsiz=w[pos];
for(auto i:G[pos])
//提前计算siz是为了减少初始化的循环次数
//不加几乎没有影响
//姑且算卡常吧(汗)
dfs(i),tsiz+=siz[i];
for(int i=w[pos];i<=min(m,tsiz);i++) f[pos][i]=v[pos];
siz[pos]=w[pos];
for(auto i:G[pos]){
for(auto j=min(m,siz[pos]+siz[i]);j>w[pos];j--){
for(int k=max(0,j-siz[pos]),lim=min(siz[i],j-w[pos]);k<=lim;k++){
f[pos][j]=max(f[pos][j],f[i][k]+f[pos][j-k]);
}
}
siz[pos]+=siz[i];
}
}4 点击查看代码
#include<bits/stdc++.h>
using namespace std;
int n,m,w[110],v[110],f[110][510];
int low[110],dfn[110],ori[110],tim;
//ori表示缩点后的位置
int n2,w2[110],v2[110];
bool vis[110],in[110];
//vis在tarjan过程中标记是否在栈中
//in记录是否有入度,用于添加0节点
int siz[110];
vector<int> G[110],G2[110];
stack<int> st;
void dfs(int pos){
int tsiz=w2[pos];
for(auto i:G2[pos])
//提前计算siz是为了减少初始化的循环次数
//不加影响不大
//姑且算卡常吧(汗)
dfs(i),tsiz+=siz[i];
for(int i=w2[pos];i<=min(m,tsiz);i++) f[pos][i]=v2[pos];
siz[pos]=w2[pos];
for(auto i:G2[pos]){
for(auto j=min(m,siz[pos]+siz[i]);j>w2[pos];j--){
for(int k=max(0,j-siz[pos]),lim=min(siz[i],j-w2[pos]);k<=lim;k++){
f[pos][j]=max(f[pos][j],f[i][k]+f[pos][j-k]);
}
}
siz[pos]+=siz[i];
}
}
void tarjan(int x){
low[x]=dfn[x]=++tim;
st.push(x);
vis[x]=1;
for(auto i:G[x]){
if(!dfn[i]){
tarjan(i);
low[x]=min(low[x],low[i]);
}else if(vis[i]){
low[x]=min(low[x],low[i]);
}
}
if(dfn[x]==low[x]){
++n2;
while(1){
int t=st.top();
ori[t]=n2;//t缩到x
st.pop();
vis[t]=0;
v2[n2]+=v[t];//累加权值
w2[n2]+=w[t];//累加大小
if(t==x) break;
}
}
}
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>w[i];
for(int i=1;i<=n;i++) cin>>v[i];
for(int i=1;i<=n;i++){
int d;
cin>>d;
if(d) G[d].emplace_back(i);
}
for(int i=1;i<=n;i++) if(!dfn[i]) tarjan(i);
for(int i=1;i<=n;i++){
int x=ori[i];
for(auto j:G[i]){
int y=ori[j];
if(x==y) continue;
G2[x].emplace_back(y);
in[y]=1;
}
}
for(int i=1;i<=n2;i++) if(!in[i]) G2[0].emplace_back(i);
dfs(0);
cout<<f[0][m];
return 0;
}时间复杂度 。