06.树链剖分

引入

树链剖分用于将树分割成若干条链的形式，以维护树上路径的信息。

具体来说，将整棵树剖分为若干条链，使它组合成线性结构，然后用其他的数据结构维护信息。

树链剖分（树剖/链剖）有多种形式，如 重链剖分，长链剖分 和用于 Link/cut Tree 的剖分（有时被称作「实链剖分」）。大多数情况下（没有特别说明时），「树链剖分」都指「重链剖分」。

重链剖分可以将树上的任意一条路径划分成不超过 $O(\log n)$ 条连续的链，每条链上的点深度互不相同（即是自底向上的一条链，链上所有点的 LCA 为链的一个端点）。

重链剖分还能保证划分出的每条链上的结点 DFS 序连续，因此可以方便地用一些维护序列的数据结构（如线段树）来维护树上路径的信息。例如：

1. 修改 树上两点之间的路径上 所有点的值。
2. 查询 树上两点之间的路径上 结点权值的 和/极值/其它（在序列上可以用数据结构维护，便于合并的信息）。

除了配合数据结构来维护树上路径信息，树剖还可以用来 $O(\log n)$（且常数较小）地求 LCA。在某些题目中，还可以利用其性质来灵活地运用树剖。

重链剖分

我们给出一些定义：

定义 重子结点 表示其子结点中子树最大的子结点。如果有多个子树最大的子结点，取其一。如果没有子结点，就无重子结点。

定义 轻子结点 表示剩余的所有子结点。

从这个结点到重子结点的边为 重边。

到其他轻子结点的边为 轻边。

若干条首尾衔接的重边构成 重链。

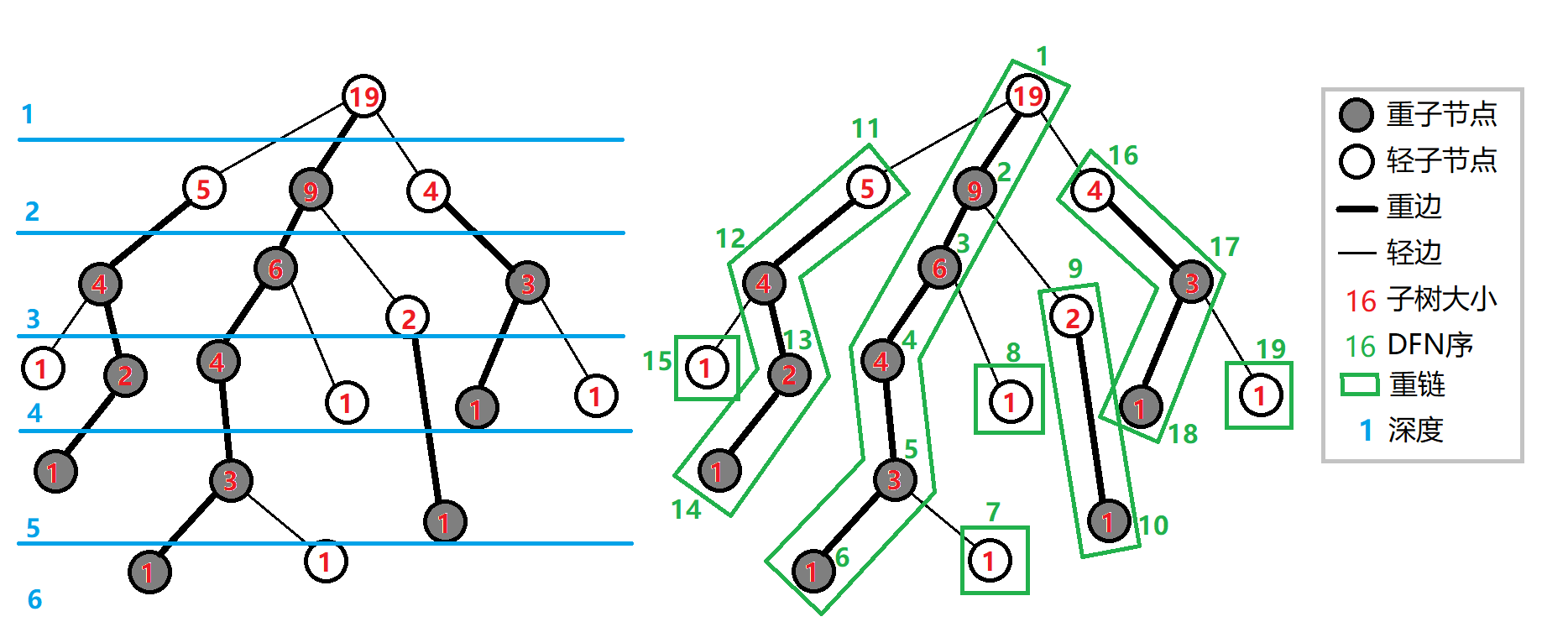
把落单的结点也当作重链，那么整棵树就被剖分成若干条重链。

如图：

实现

树剖的实现分两个 DFS 的过程。伪代码如下：

第一个 DFS 记录每个结点的父结点（$\text{father}$）、深度（$\text{depth}$）、子树大小（$\text{size}$）、重子结点（$\text{hson}$）。

$$\begin{array}{l}\text{TREE-BUILD }(u,\text{dep})\\ \begin{array}{ll}1& u.\text{hson}\leftarrow 0\\ 2& u.\text{hson}.\text{size}\leftarrow 0\\ 3& u.\text{depth}\leftarrow \text{dep}\\ 4& u.\text{size}\leftarrow 1\\ 5& \text{for }\text{each son }v\text{ of }u\\ 6& u.\text{size}\leftarrow u.\text{size}+\text{TREE-BUILD }(v,\text{dep}+1)\\ 7& v.\text{father}\leftarrow u\\ 8& \text{if }v.\text{size}>u.\text{hson}.\text{size}\\ 9& u.\text{hson}\leftarrow v\\ 10& \text{return }u.\text{size}\end{array}\end{array}$$

第二个 DFS 记录所在链的链顶（$\text{top}$，应初始化为结点本身）、重边优先遍历时的 DFS 序（$\text{top}$）、DFS 序对应的结点编号（$\text{rank}$）。

$$\begin{array}{l}\text{TREE-DECOMPOSITION }(u,\text{top})\\ \begin{array}{ll}1& u.\text{top}\leftarrow \text{top}\\ 2& \text{tot}\leftarrow \text{tot}+1\\ 3& u.\text{dfn}\leftarrow \text{tot}\\ 4& \text{rank}(\text{tot})\leftarrow u\\ 5& \text{if }u.\text{hson}\text{ is not }0\\ 6& \text{TREE-DECOMPOSITION }(u.\text{hson},\text{top})\\ 7& \text{for }\text{each son }v\text{ of }u\\ 8& \text{if }v\text{ is not }u.\text{hson}\\ 9& \text{TREE-DECOMPOSITION }(v,v)\end{array}\end{array}$$

以下为代码实现。

我们先给出一些定义：

• $\mathrm{fa}(x)$ 表示结点 $x$ 在树上的父亲。
• $\mathrm{dep}(x)$ 表示结点 $x$ 在树上的深度。
• $\mathrm{siz}(x)$ 表示结点 $x$ 的子树的结点个数。
• $\mathrm{son}(x)$ 表示结点 $x$ 的 重儿子。
• $\mathrm{top}(x)$ 表示结点 $x$ 所在 重链 的顶部结点（深度最小）。
• $\mathrm{dfn}(x)$ 表示结点 $x$ 的 DFS 序，也是其在线段树中的编号。
• $\mathrm{rnk}(x)$ 表示 DFS 序所对应的结点编号，有 $\mathrm{rnk}(\mathrm{dfn}(x))=x$。

我们进行两遍 DFS 预处理出这些值，其中第一次 DFS 求出 $\mathrm{fa}(x)$，$\mathrm{dep}(x)$，$\mathrm{siz}(x)$，$\mathrm{son}(x)$，第二次 DFS 求出 $\mathrm{top}(x)$，$\mathrm{dfn}(x)$，$\mathrm{rnk}(x)$。

void dfs1(int u, int f) {
  fa[u] = f, dep[u] = dep[f] + 1, siz[u] = 1;
  for (auto v : G[u]) {
    if (v == f) continue;
    dfs1(v, u);
    siz[u] += siz[v];
    if (siz[v] > siz[son[u]]) son[u] = v;
  }
}
 
void dfs2(int u, int ftop) {
  top[u] = ftop, dfn[u] = ++idx, rnk[idx] = u;
  if (son[u]) dfs2(son[u], ftop);
  for (auto v : G[u])
    if (v != son[u] && v != fa[u]) dfs2(v, v);
}

重链剖分的性质

树上每个结点都属于且仅属于一条重链。

重链开头的结点不一定是重子结点（因为重边是对于每一个结点都有定义的）。

所有的重链将整棵树 完全剖分。

在剖分时 重边优先遍历，最后树的 DFS 序上，重链内的 DFS 序是连续的。按 DFN 排序后的序列即为剖分后的链。

一棵子树内的 DFS 序是连续的。

可以发现，当我们向下经过一条 轻边 时，所在子树的大小至少会除以二。

因此，对于树上的任意一条路径，把它拆分成从 LCA 分别向两边往下走，分别最多走 $O(\log n)$ 次，因此，树上的每条路径都可以被拆分成不超过 $O(\log n)$ 条重链。

怎么有理有据地卡树剖

一般情况下树剖的 $O(\log n)$ 常数不满很难卡，如果要卡只能建立二叉树深度低。

于是我们可以考虑折中方案。

我们建立一棵 $\sqrt{n}$ 个结点的二叉树。对于每个结点到其儿子的边，我们将其替换成一条长度为 $\sqrt{n}$ 的链。

这样子我们可以将随机询问轻重链切换次数卡到平均 $\frac{\log n}{2}$ 次，同时有 $O(\sqrt{n}\log n)$ 的深度。

加上若干随机叶子看上去可以卡树剖。但是树剖常数小有可能卡不掉。

常见应用

路径上维护

用树链剖分求树上两点路径权值和，伪代码如下：

$$\begin{array}{l}\text{TREE-PATH-SUM }(u,v)\\ \begin{array}{ll}1& \text{tot}\leftarrow 0\\ 2& \text{while }u.\text{top}\text{ is not }v.\text{top}\\ 3& \text{if }u.\text{top}.\text{depth}<v.\text{top}.\text{depth}\\ 4& \text{SWAP}(u,v)\\ 5& \text{tot}\leftarrow \text{tot}+\text{sum of values between }u\text{ and }u.\text{top}\\ 6& u\leftarrow u.\text{top}.\text{father}\\ 7& \text{tot}\leftarrow \text{tot}+\text{sum of values between }u\text{ and }v\\ 8& \text{return }\text{tot}\end{array}\end{array}$$

链上的 DFS 序是连续的，可以使用线段树、树状数组维护。

每次选择深度较大的链往上跳，直到两点在同一条链上。

同样的跳链结构适用于维护、统计路径上的其他信息。

子树维护

有时会要求，维护子树上的信息，譬如将以 $x$ 为根的子树的所有结点的权值增加 $v$。

在 DFS 搜索的时候，子树中的结点的 DFS 序是连续的。

每一个结点记录 bottom 表示所在子树连续区间末端的结点。

这样就把子树信息转化为连续的一段区间信息。

求最近公共祖先

不断向上跳重链，当跳到同一条重链上时，深度较小的结点即为 LCA。

向上跳重链时需要先跳所在重链顶端深度较大的那个。

参考代码：

int lca(int u, int v) {
  while (top[u] != top[v]) {
    if (dep[top[u]] > dep[top[v]])
      u = fa[top[u]];
    else
      v = fa[top[v]];
  }
  return dep[u] > dep[v] ? v : u;
}

换根操作

考虑一类新的问题：除了树链剖分支持的基本操作外，加上了换根操作。

由于树链剖分维护的信息是静态的，不支持动态修改。同时，不可能每次换根后重新预处理信息，复杂度过高。那么，需要充分利用之前得到的信息来帮助解决换根操作。

对于路径修改和查询操作，由于树上两点之间的简单路径唯一，所以不会发生变化，与正常的处理方式相同。

对于子树修改和查询操作，一般的思路就是将换根后的子树映射到原来的子树。这需要分类讨论操作子树的根结点、换根后的整个树的根结点，以及原来树的根结点的相对位置关系。具体细节详见 后文例题。

例题

本文通过例题展示如何应用重链剖分。首先是一道模板题。

「ZJOI2008」树的统计

对一棵有 $n$ 个结点，结点带权值的静态树，进行三种操作共 $q$ 次：

1. 修改单个结点的权值；
2. 查询 $u$ 到 $v$ 的路径上的最大权值；
3. 查询 $u$ 到 $v$ 的路径上的权值之和。

保证 $1\le n\le 30000$，$0\le q\le 200000$。

解答

根据题面以及前文所述性质，线段树需要维护三种操作：

1. 单点修改；
2. 区间查询最大值；
3. 区间查询和。

单点修改很容易实现。

由于子树的 DFS 序连续（无论是否树剖都是如此），修改一个结点的子树只用修改这一段连续的 DFS 序区间。

问题是如何修改/查询两个结点之间的路径。

考虑我们是如何用 倍增法求解 LCA 的。首先我们 将两个结点提到同一高度，然后将两个结点一起向上跳。对于树链剖分也可以使用这样的思想。

在向上跳的过程中，如果当前结点在重链上，向上跳到重链顶端，如果当前结点不在重链上，向上跳一个结点。如此直到两结点相同。沿途更新/查询区间信息。

对于每个询问，最多经过 $O(\log n)$ 条重链，每条重链上线段树的复杂度为 $O(\log n)$，因此总时间复杂度为 $O(n\log n+q{\log }^{2}n)$。实际上重链个数很难达到 $O(\log n)$（可以用完全二叉树卡满），所以树剖在一般情况下常数较小。

参考代码

#include <algorithm>
#include <cstring>
#include <iostream>
#define lc o << 1
#define rc o << 1 | 1
constexpr int MAXN = 60010;
constexpr int inf = 2e9;
int n, a, b, w[MAXN], q, u, v;
int cur, h[MAXN], nxt[MAXN], p[MAXN];
int siz[MAXN], top[MAXN], son[MAXN], dep[MAXN], fa[MAXN], dfn[MAXN], rnk[MAXN],
    cnt;
char op[10];
 
void add_edge(int x, int y) {  // 加边
  cur++;
  nxt[cur] = h[x];
  h[x] = cur;
  p[cur] = y;
}
 
struct SegTree {
  int sum[MAXN * 4], maxx[MAXN * 4];
 
  void build(int o, int l, int r) {
    if (l == r) {
      sum[o] = maxx[o] = w[rnk[l]];
      return;
    }
    int mid = (l + r) >> 1;
    build(lc, l, mid);
    build(rc, mid + 1, r);
    sum[o] = sum[lc] + sum[rc];
    maxx[o] = std::max(maxx[lc], maxx[rc]);
  }
 
  int query1(int o, int l, int r, int ql, int qr) {  // 查询 max
    if (l > qr || r < ql) return -inf;
    if (ql <= l && r <= qr) return maxx[o];
    int mid = (l + r) >> 1;
    return std::max(query1(lc, l, mid, ql, qr), query1(rc, mid + 1, r, ql, qr));
  }
 
  int query2(int o, int l, int r, int ql, int qr) {  // 查询 sum
    if (l > qr || r < ql) return 0;
    if (ql <= l && r <= qr) return sum[o];
    int mid = (l + r) >> 1;
    return query2(lc, l, mid, ql, qr) + query2(rc, mid + 1, r, ql, qr);
  }
 
  void update(int o, int l, int r, int x, int t) {  // 更新
    if (l == r) {
      maxx[o] = sum[o] = t;
      return;
    }
    int mid = (l + r) >> 1;
    if (x <= mid)
      update(lc, l, mid, x, t);  // 左右分别更新
    else
      update(rc, mid + 1, r, x, t);
    sum[o] = sum[lc] + sum[rc];
    maxx[o] = std::max(maxx[lc], maxx[rc]);
  }
} st;
 
void dfs1(int o) {
  son[o] = -1;
  siz[o] = 1;
  for (int j = h[o]; j; j = nxt[j])
    if (!dep[p[j]]) {
      dep[p[j]] = dep[o] + 1;
      fa[p[j]] = o;
      dfs1(p[j]);
      siz[o] += siz[p[j]];
      if (son[o] == -1 || siz[p[j]] > siz[son[o]]) son[o] = p[j];
    }
}
 
void dfs2(int o, int t) {
  top[o] = t;
  cnt++;
  dfn[o] = cnt;
  rnk[cnt] = o;
  if (son[o] == -1) return;
  dfs2(son[o], t);
  for (int j = h[o]; j; j = nxt[j])
    if (p[j] != son[o] && p[j] != fa[o]) dfs2(p[j], p[j]);
}
 
int querymax(int x, int y) {  // 查询，看main函数理解一下
  int ret = -inf, fx = top[x], fy = top[y];
  while (fx != fy) {
    if (dep[fx] >= dep[fy])
      ret = std::max(ret, st.query1(1, 1, n, dfn[fx], dfn[x])), x = fa[fx];
    else
      ret = std::max(ret, st.query1(1, 1, n, dfn[fy], dfn[y])), y = fa[fy];
    fx = top[x];
    fy = top[y];
  }
  if (dfn[x] < dfn[y])
    ret = std::max(ret, st.query1(1, 1, n, dfn[x], dfn[y]));
  else
    ret = std::max(ret, st.query1(1, 1, n, dfn[y], dfn[x]));
  return ret;
}
 
int querysum(int x, int y) {
  int ret = 0, fx = top[x], fy = top[y];
  while (fx != fy) {
    if (dep[fx] >= dep[fy])
      ret += st.query2(1, 1, n, dfn[fx], dfn[x]), x = fa[fx];
    else
      ret += st.query2(1, 1, n, dfn[fy], dfn[y]), y = fa[fy];
    fx = top[x];
    fy = top[y];
  }
  if (dfn[x] < dfn[y])
    ret += st.query2(1, 1, n, dfn[x], dfn[y]);
  else
    ret += st.query2(1, 1, n, dfn[y], dfn[x]);
  return ret;
}
 
using std::cin;
using std::cout;
 
int main() {
  cin.tie(nullptr)->sync_with_stdio(false);
  cin >> n;
  for (int i = 1; i < n; i++) cin >> a >> b, add_edge(a, b), add_edge(b, a);
  for (int i = 1; i <= n; i++) cin >> w[i];
  dep[1] = 1;
  dfs1(1);
  dfs2(1, 1);
  st.build(1, 1, n);
  cin >> q;
  while (q--) {
    cin >> op >> u >> v;
    if (!strcmp(op, "CHANGE")) st.update(1, 1, n, dfn[u], v);
    if (!strcmp(op, "QMAX")) cout << querymax(u, v) << '\n';
    if (!strcmp(op, "QSUM")) cout << querysum(u, v) << '\n';
  }
  return 0;
}

然后是一道带换根操作的重链剖分模板题。

LOJ 139. 树链剖分

给定一棵 $n$ 个结点的树（初始根结点为 $1$），要求支持如下的 $m$ 次操作：

• 换根，将结点 $u$ 设为新的树根。
• 修改路径上结点权值，将结点 $u$ 和结点 $v$ 之间路径上的所有结点（包括这两个结点）的权值增加 $w$。
• 修改子树上结点权值，将以结点 $u$ 为根的子树上的所有结点的权值增加 $w$。
• 询问路径，询问结点 $u$ 和结点 $v$ 之间路径上的所有结点（包括这两个结点）的权值和。
• 询问子树，询问以结点 $u$ 为根的子树上的所有结点的权值和。

$1\le n,m\le 10^5$。

解法

先以 $1$ 作为根结点跑 DFS，预处理出树链剖分所必需的信息。为方便表述，称以 $1$ 为根结点的树为「原始树」，而称经历了若干次换根操作之后的树为「当前树」。在操作过程中，需要维护 $\text{root}$ 为当前树的根结点。由于线段树中存储的是原始树的 DFS 序的信息，所以每次查询和修改时，都需要将当前树的查询和修改操作转换到原始树上。

对于换根操作，我们直接令 $\text{root}\leftarrow u$。对于路径操作，由于换根不影响路径，所以直接在原始树上做对应操作即可。

重点考虑操作子树的问题。我们根据 $u$ 和 $\text{root}$ 的相对位置关系做分类讨论：

• $u=\text{root}$：这是最特殊的情况，相当于对整棵树做操作。为此，直接对线段树的根结点打上标记或查询答案即可。

• $u$ 是 $\text{root}$ 在原始树上的祖先，即 $u$ 位于 $1$ 到 $\text{root}$ 的简单路径上。

  这是最值得注意的情况。定义 $v$ 为原始树上 $u$ 到 $\text{root}$ 的简单路径上除 $u$ 以外的深度最小的点，可以发现原始树上 $v$ 及其子树以外的部分恰好是当前树上 $u$ 及其子树。

  考虑如何高效找到 $v$。我们先令 $v\leftarrow \text{root}$，然后沿着重链往上跳直到 $\mathrm{dep}(\mathrm{top}(v))\le \mathrm{dep}(u)+1$。

  • 若 $\mathrm{dep}(\mathrm{top}(v))=\mathrm{dep}(u)+1$，令 $v\leftarrow \mathrm{top}(v)$。此时，$v$ 是 $u$ 的一个轻儿子。
  • 若 $\mathrm{dep}(\mathrm{top}(v))<\mathrm{dep}(u)+1$，亦即 $\mathrm{dep}(\mathrm{top}(v))\le \mathrm{dep}(u)$，这说明 $u,v$ 处在同一条重链上。根据同一条重链上 DFS 序连续的性质，所求的 $v$ 必然满足 $\mathrm{dfn}(v)=\mathrm{dfn}(u)+1$。所以，可以令 $v\leftarrow \mathrm{rnk}(\mathrm{dfn}(u)+1)$。

  注意，这两种情形中可以合并：在跳完之后可以直接令

  $$v\leftarrow \mathrm{rnk}(\mathrm{dfn}(\mathrm{top}(v))+\mathrm{dep}(u)+1-\mathrm{dep}(\mathrm{top}(v))).$$

  容易验证，利用这一表达式找到的 $v$，和分类讨论找到的 $v$ 是等价的。参考实现中就用到了这一表达式。

  由于 $v$ 子树覆盖的区间为 $[\mathrm{dfn}(v),\mathrm{dfn}(v)+\mathrm{siz}(v))$，所以只需要对 $[1,\mathrm{dfn}(v))\cup [\mathrm{dfn}(v)+\mathrm{siz}(v),n]$ 操作即可。

• 其它情况。可以发现换根操作不会影响 $u$ 的子树，用正常的方式维护即可。

这样做的复杂度与不带换根的做法相同，均为 $O(n{\log }^{2}n)$。

参考代码

#include <iostream>
#include <vector>
 
using lint = long long;
constexpr int N = 1e5 + 10;
 
int n, m, root, a[N];
std::vector<int> G[N];
 
int idx, fa[N], dep[N], siz[N], son[N], top[N], dfn[N], rnk[N];
 
struct SegmentTree {  // 区间加，区间求和的线段树实现
  lint sum[N << 2], lzy[N << 2];
 
  void maketag(int u, int l, int r, lint x) {
    sum[u] += (r - l + 1) * x;
    lzy[u] += x;
  }
 
  void pushup(int u) { sum[u] = sum[u << 1] + sum[u << 1 | 1]; }
 
  void pushdown(int u, int l, int r) {
    int mid = l + r >> 1;
    maketag(u << 1, l, mid, lzy[u]);
    maketag(u << 1 | 1, mid + 1, r, lzy[u]);
    lzy[u] = 0;
  }
 
  void build(int u, int l, int r) {
    if (l == r) {
      sum[u] = a[rnk[l]];
      return;
    }
    int mid = l + r >> 1;
    build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
    pushup(u);
  }
 
  void upd(int u, int l, int r, int ql, int qr, lint x) {
    if (ql <= l && r <= qr) {
      maketag(u, l, r, x);
      return;
    }
    int mid = l + r >> 1;
    pushdown(u, l, r);
    if (ql <= mid) upd(u << 1, l, mid, ql, qr, x);
    if (qr > mid) upd(u << 1 | 1, mid + 1, r, ql, qr, x);
    pushup(u);
  }
 
  lint ask(int u, int l, int r, int ql, int qr) {
    if (ql <= l && r <= qr) return sum[u];
    int mid = l + r >> 1;
    pushdown(u, l, r);
    if (qr <= mid) return ask(u << 1, l, mid, ql, qr);
    if (ql > mid) return ask(u << 1 | 1, mid + 1, r, ql, qr);
    return ask(u << 1, l, mid, ql, qr) + ask(u << 1 | 1, mid + 1, r, ql, qr);
  }
} T;
 
void dfs1(int u, int f) {  // 树剖预处理 1
  fa[u] = f, dep[u] = dep[f] + 1, siz[u] = 1;
  for (auto v : G[u]) {
    if (v == f) continue;
    dfs1(v, u);
    siz[u] += siz[v];
    if (siz[v] > siz[son[u]]) son[u] = v;
  }
}
 
void dfs2(int u, int tp) {  // 树剖预处理 2
  top[u] = tp, dfn[u] = ++idx, rnk[idx] = u;
  if (son[u]) dfs2(son[u], tp);
  for (auto v : G[u])
    if (v != fa[u] && v != son[u]) dfs2(v, v);
}
 
void modify_path(int u, int v, int w) {  // 正常树剖
  while (top[u] != top[v]) {
    if (dep[top[u]] < dep[top[v]]) std::swap(u, v);
    T.upd(1, 1, n, dfn[top[u]], dfn[u], w);
    u = fa[top[u]];
  }
  if (dep[u] < dep[v]) std::swap(u, v);
  T.upd(1, 1, n, dfn[v], dfn[u], w);
}
 
void modify_subtree(int u, int w) {
  if (u == root)
    T.maketag(1, 1, n, w);
  else if (dfn[u] <= dfn[root] && dfn[root] <= dfn[u] + siz[u] - 1) {
    int v = root;
    while (dep[top[v]] > dep[u] + 1) v = fa[top[v]];  // 向上跳
    v = rnk[dfn[top[v]] + dep[u] + 1 - dep[top[v]]];  // 计算 v
    // 上面这一句可以替换为如下两句：
    // if (dep[top[v]] == dep[u] + 1) v = top[v];
    // else if (dep[top[v]] < dep[u] + 1) v = rnk[dfn[u] + 1];
    if (1 <= dfn[v] - 1) T.upd(1, 1, n, 1, dfn[v] - 1, w);
    if (dfn[v] + siz[v] <= n) T.upd(1, 1, n, dfn[v] + siz[v], n, w);
  } else
    T.upd(1, 1, n, dfn[u], dfn[u] + siz[u] - 1, w);
}
 
lint query_path(int u, int v) {  // 正常树剖
  lint res = 0;
  while (top[u] != top[v]) {
    if (dep[top[u]] < dep[top[v]]) std::swap(u, v);
    res += T.ask(1, 1, n, dfn[top[u]], dfn[u]);
    u = fa[top[u]];
  }
  if (dep[u] < dep[v]) std::swap(u, v);
  res += T.ask(1, 1, n, dfn[v], dfn[u]);
  return res;
}
 
lint query_subtree(int u) {
  if (u == root) return T.sum[1];
  if (dfn[u] <= dfn[root] && dfn[root] <= dfn[u] + siz[u] - 1) {
    int v = root;
    while (dep[top[v]] > dep[u] + 1) v = fa[top[v]];
    v = rnk[dfn[top[v]] + dep[u] + 1 - dep[top[v]]];
    lint res = 0;
    if (1 <= dfn[v] - 1) res += T.ask(1, 1, n, 1, dfn[v] - 1);
    if (dfn[v] + siz[v] <= n) res += T.ask(1, 1, n, dfn[v] + siz[v], n);
    return res;
  }
  return T.ask(1, 1, n, dfn[u], dfn[u] + siz[u] - 1);
}
 
int main() {
  std::cin.tie(nullptr)->sync_with_stdio(false);
  std::cin >> n, root = 1;
  for (int i = 1; i <= n; ++i) std::cin >> a[i];
  for (int i = 2, f; i <= n; ++i) {
    std::cin >> f;
    G[i].emplace_back(f);
    G[f].emplace_back(i);
  }
  dfs1(1, 0), dfs2(1, 1), T.build(1, 1, n);  // 预处理
  for (std::cin >> m; m; --m) {
    int op, u, v, w;
    std::cin >> op >> u;
    if (op == 1)
      root = u;  // 换根
    else if (op == 2)
      std::cin >> v >> w, modify_path(u, v, w);  // 修改路径
    else if (op == 3)
      std::cin >> w, modify_subtree(u, w);  // 修改子树
    else if (op == 4)
      std::cin >> v, std::cout << query_path(u, v) << "\n";  // 查询路径
    else
      std::cout << query_subtree(u) << "\n";  // 查询子树
  }
  std::cout.flush();
  return 0;
}

最后是一道交互题，也是树剖的非传统应用。

Nauuo and Binary Tree

有一棵以 $1$ 为根的二叉树，你可以询问任意两点之间的距离，求出每个点的父亲。

结点数不超过 $3000$，你最多可以进行 $30000$ 次询问。

解法

首先可以通过 $n-1$ 次询问确定每个结点的深度。

然后考虑按深度从小到大确定每个结点的父亲，这样的话确定一个结点的父亲时其所有祖先一定都是已知的。

确定一个结点的父亲之前，先对树已知的部分进行重链剖分。

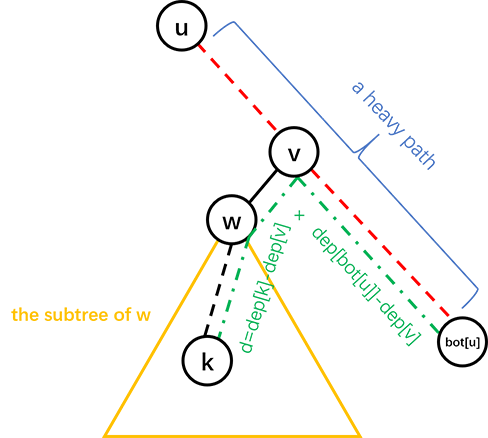
假设我们需要在子树 $u$ 中找结点 $k$ 所在的位置，我们可以询问 $k$ 与 $u$ 所在重链的尾端的距离，就可以进一步确定 $k$ 的位置，具体见图：

其中红色虚线是一条重链，$d$ 是询问的结果即 $\text{dis}(k,\text{bot}(u))$，$v$ 的深度为 $(\text{dep}(k)+\text{dep}(\text{bot}(u))-d)/2$。

这样的话，如果 $v$ 只有一个儿子，$k$ 的父亲就是 $v$，否则可以递归地在 $w$ 的子树中找 $k$ 的父亲。

时间复杂度 $O(n^2)$，询问复杂度 $O(n\log n)$。

具体地，设 $T(n)$ 为最坏情况下在一棵大小为 $n$ 的树中找到一个新结点的位置所需的询问次数，可以得到：

$$T(n)\le \{\begin{array}{ll}0& n=1\\ T\left(\lfloor \frac{n-1}{2}\rfloor \right)+1& n\ge 2\end{array}$$

$2999+{\sum }_{i=1}^{2999}T(i)\le 29940$，事实上这个上界是可以通过构造数据达到的，然而只要进行一些随机扰动（如对深度进行排序时使用不稳定的排序算法），询问次数很难超过 $21000$ 次。

参考代码

#include <algorithm>
#include <cstdio>
#include <iostream>
 
using namespace std;
 
constexpr int N = 3010;
 
int n, fa[N], ch[N][2], dep[N], siz[N], son[N], bot[N], id[N];
 
int query(int u, int v) {
  printf("? %d %d\n", u, v);
  fflush(stdout);
  int d;
  scanf("%d", &d);
  return d;
}
 
void setFather(int u, int v) {
  fa[v] = u;
  if (ch[u][0])
    ch[u][1] = v;
  else
    ch[u][0] = v;
}
 
void dfs(int u) {
  if (ch[u][0]) dfs(ch[u][0]);
  if (ch[u][1]) dfs(ch[u][1]);
 
  siz[u] = siz[ch[u][0]] + siz[ch[u][1]] + 1;
 
  if (ch[u][1])
    son[u] = int(siz[ch[u][0]] < siz[ch[u][1]]);
  else
    son[u] = 0;
 
  if (ch[u][son[u]])
    bot[u] = bot[ch[u][son[u]]];
  else
    bot[u] = u;
}
 
void solve(int u, int k) {
  if (!ch[u][0]) {
    setFather(u, k);
    return;
  }
  int d = query(k, bot[u]);
  int v = bot[u];
  while (dep[v] > (dep[k] + dep[bot[u]] - d) / 2) v = fa[v];
  int w = ch[v][son[v] ^ 1];
  if (w)
    solve(w, k);
  else
    setFather(v, k);
}
 
int main() {
  int i;
 
  scanf("%d", &n);
 
  for (i = 2; i <= n; ++i) {
    id[i] = i;
    dep[i] = query(1, i);
  }
 
  sort(id + 2, id + n + 1, [](int x, int y) { return dep[x] < dep[y]; });
 
  for (i = 2; i <= n; ++i) {
    dfs(1);
    solve(1, id[i]);
  }
 
  printf("!");
  for (i = 2; i <= n; ++i) printf(" %d", fa[i]);
  printf("\n");
  fflush(stdout);
 
  return 0;
}

长链剖分

长链剖分本质上就是另外一种链剖分方式。

定义 重子结点 表示其子结点中子树深度最大的子结点。如果有多个子树最大的子结点，取其一。如果没有子结点，就无重子结点。

定义 轻子结点 表示剩余的子结点。

从这个结点到重子结点的边为 重边。

到其他轻子结点的边为 轻边。

若干条首尾衔接的重边构成 重链。

把落单的结点也当作重链，那么整棵树就被剖分成若干条重链。

如图（这种剖分方式既可以看成重链剖分也可以看成长链剖分）：

长链剖分实现方式和重链剖分类似，这里就不再展开。

常见应用

首先，我们发现长链剖分从一个结点到根的路径的轻边切换条数是 $\sqrt{n}$ 级别的。

如何构造数据将轻重边切换次数卡满

我们可以构造这么一棵二叉树 T：

假设构造的二叉树参数为 $D$。

若 $D\ne 0$, 则在左儿子构造一棵参数为 $D-1$ 的二叉树，在右儿子构造一个长度为 $2D-1$ 的链。

若 $D=0$, 则我们可以直接构造一个单独叶结点，并且结束调用。

这样子构造一定可以将单独叶结点到根的路径全部为轻边且需要 $D^2$ 级别的结点数。

取 $D=\sqrt{n}$ 即可。

长链剖分优化 DP

一般情况下可以使用长链剖分来优化的 DP 会有一维状态为深度维。

我们可以考虑使用长链剖分优化树上 DP。

具体的，我们每个结点的状态直接继承其重儿子的结点状态，同时将轻儿子的 DP 状态暴力合并。

Codeforces 1009 F. Dominant Indices

给定一棵有 $n$ 个顶点的有根树，以顶点 $1$ 作为根。

定义顶点 $x$ 的深度数组为一个无限序列 $[d_{x,0},d_{x,1},d_{x,2},\dots ]$，其中 $d_{x,i}$ 表示满足以下两个条件的顶点 $y$ 的数量：

• $x$ 是 $y$ 的祖先；
• 从 $x$ 到 $y$ 的简单路径恰好经过 $i$ 条边。

顶点 $x$ 的深度数组的主导下标（dominant index）（简称顶点 $x$ 的主导下标）定义为一个下标 $j$，满足：

• 对于所有 $k<j$，都有 $d_{x,k}<d_{x,j}$；
• 对于所有 $k>j$，都有 $d_{x,k}\le d_{x,j}$。

请计算树中每个顶点的主导下标。

解答

我们设 $f_{i,j}$ 表示在子树 i 内，和 i 距离为 j 的点数。

直接暴力转移时间复杂度为 $O(n^2)$

我们考虑每次转移我们直接继承重儿子的 DP 数组和答案，并且考虑在此基础上进行更新。

首先我们需要将重儿子的 DP 数组前面插入一个元素 1, 这代表着当前结点。

然后我们将所有轻儿子的 DP 数组暴力和当前结点的 DP 数组合并。

注意到因为轻儿子的 DP 数组长度为轻儿子所在重链长度，而所有重链长度和为 $n$。

也就是说，我们直接暴力合并轻儿子的总时间复杂度为 $O(n)$。

参考代码

#include <algorithm>
#include <iostream>
using namespace std;
constexpr int N = 1000005;
 
struct edge {
  int to, next;
} e[N * 2];
 
int head[N], tot, n;
int d[N], fa[N], mx[N];
int *f[N], g[N], mxp[N];
int dfn[N];
 
void add(int x, int y) {
  e[++tot] = edge{y, head[x]};
  head[x] = tot;
}
 
void dfs1(int x) {  // 第一次插入一个1
  d[x] = 1;
  for (int i = head[x]; i; i = e[i].next)
    if (e[i].to != fa[x]) {
      fa[e[i].to] = x;
      dfs1(e[i].to);
      d[x] = max(d[x], d[e[i].to] + 1);
      if (d[e[i].to] > d[mx[x]]) mx[x] = e[i].to;
    }
}
 
void dfs2(int x) {  // 第二次合并
  dfn[x] = ++*dfn;
  f[x] = g + dfn[x];
  if (mx[x]) dfs2(mx[x]);
  for (int i = head[x]; i; i = e[i].next)
    if (e[i].to != fa[x] && e[i].to != mx[x]) dfs2(e[i].to);
}
 
void getans(int x) {  // 暴力合并算答案
  if (mx[x]) {
    getans(mx[x]);
    mxp[x] = mxp[mx[x]] + 1;
  }
  f[x][0] = 1;
  if (f[x][mxp[x]] <= 1) mxp[x] = 0;
  for (int i = head[x]; i; i = e[i].next)
    if (e[i].to != fa[x] && e[i].to != mx[x]) {
      getans(e[i].to);
      int len = d[e[i].to];
      for (int j = 0; j <= len - 1; j++) {
        f[x][j + 1] += f[e[i].to][j];
        if (f[x][j + 1] > f[x][mxp[x]]) mxp[x] = j + 1;
        if (f[x][j + 1] == f[x][mxp[x]] && j + 1 < mxp[x]) mxp[x] = j + 1;
      }
    }
}
 
int main() {
  cin.tie(nullptr)->sync_with_stdio(false);
  cin >> n;
  for (int i = 1; i < n; i++) {
    int x, y;
    cin >> x >> y;
    add(x, y);
    add(y, x);
  }
  dfs1(1);
  dfs2(1);
  getans(1);
  for (int i = 1; i <= n; i++) cout << mxp[i] << '\n';
}

注意，一般情况下 DP 数组的内存分配为一条重链整体分配内存，链上不同的结点有不同的首位置指针。

DP 数组的长度我们可以根据子树最深结点算出。

当然长链剖分优化 DP 技巧非常多，包括但是不仅限于打标记等等。这里不再展开。

参考 租酥雨的博客。

长链剖分求 k 级祖先

即询问一个点向父亲跳 $k$ 次跳到的结点。

首先我们假设我们已经预处理了每一个结点的 $2^i$ 级祖先。

现在我们假设我们找到了询问结点的 $2^i$ 级祖先满足 $2^i\le k<2^{i+1}$。

我们考虑求出其所在重链的结点并且按照深度列入表格。假设重链长度为 $d$。

同时我们在预处理的时候找到每条重链的根结点的 $1$ 到 $d$ 级祖先，同样放入表格。

根据长链剖分的性质，$k-2^i\le 2^i\le d$, 也就是说，我们可以 $O(1)$ 在这条重链的表格上求出的这个结点的 $k$ 级祖先。

预处理需要倍增出 $2^i$ 次级祖先，同时需要预处理每条重链对应的表格。

预处理复杂度 $O(n\log n)$, 询问复杂度 $O(1)$。

习题

• 「洛谷 P3379」【模板】最近公共祖先（LCA）（树剖求 LCA 无需数据结构，可以用作练习）
• 「JLOI2014」松鼠的新家（当然也可以用树上差分）
• 「HAOI2015」树上操作
• 「洛谷 P3384」【模板】重链剖分/树链剖分
• 「洛谷 P1505」[国家集训队] 旅游
• 「NOI2015」软件包管理器
• 「SDOI2011」染色
• 「SDOI2014」旅行
• 「洛谷 P3979」遥远的国度
• 「POI2014」Hotel 加强版（长链剖分优化 DP）
• 攻略（长链剖分优化贪心）